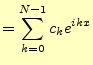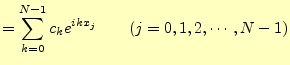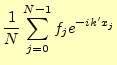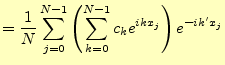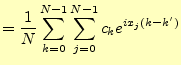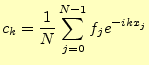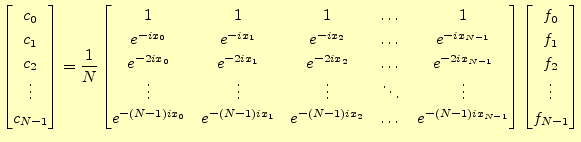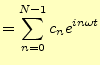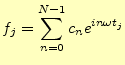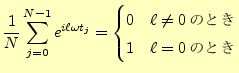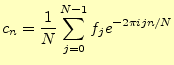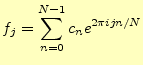1 離散フーリエ変換
ここでの離散フーリエ変換の説明については、参考文献 [1]を大いに
参考にした。
1.1 区間
![$ {\boldsymbol [0,\,2\pi]}$](img3.png) の場合
の場合
数学で学習するフーリエ変換は、連続的な関数を対象にする。しかし実際の測定量、例え
ば電圧などは離散データであることの方が圧倒的に多い。そこで、このような離散的なデー
タを計算機でフーリエ変換することを考える。これを離散フーリエ変換と言い、コンピュー
ターが得意とする分野である。フーリエ変換という名前が付いているが、実際には
フーリエ級数に近い。これからの説明は、フーリエ級数の展開係数を求めたことを思
い出しながら読めば理解しやすいであろう。
フーリエ級数では周期が重要であったが、離散フーリエ変換ではデータの区間がそれ
に対応する。任意の区間については後ほど述べることとし、まずは話
を簡単にするためにそれが![]() の場合を考える。0〜
の場合を考える。0〜![]() 秒の間で電圧を測定した
ようなものである。離散フーリエ変換の結果をこの区間を越えて拡張する場合2、区間
秒の間で電圧を測定した
ようなものである。離散フーリエ変換の結果をこの区間を越えて拡張する場合2、区間 ![]() と同じ
周期が現れる。
と同じ
周期が現れる。
この区間で ![]() 個の等間隔でデータが得られた考える。等間隔という
ことは重要で、それを
個の等間隔でデータが得られた考える。等間隔という
ことは重要で、それを
| (1) |
と表す。一方、従属変数の方は、
| (2) |
と表現することにする。実験データでは、
ここでは、測定量
![]() の組は
の組は ![]() 個ある。この
個ある。この ![]() 個のデータを操作して、
得られる1次独立なデータ数は最大
個のデータを操作して、
得られる1次独立なデータ数は最大 ![]() 個である。このことから、フーリエ係数は
個である。このことから、フーリエ係数は ![]() 個が限界
であることが分かる。従って、展開の基底も
個が限界
であることが分かる。従って、展開の基底も ![]() 個となり、それを
個となり、それを
| (3) |
のように選ぶ。基底の線形和として、元の関数
として表すことができる。このように三角関数の和で表すことを、フーリエ級数と言うの である。ここで残された問題は、測定量の
の連立方程式を解けばよろしい。この式の形が分かりにくい。それではもう少 し分かり易く書いてみよう。
「なるほど、連立方程式ならば計算機は得意なので、式(6)を解
けば話は終わり」と思ってしまうかもしれないが、そんなに世の中は甘くない。![]() 位になるとこの式を計算するのにかなりの時間がかかり実用に適さない。実際、FFTを使
いたい場面ではリアルタイム(少なくとも1秒くらい)で計測が終わる必要があるので、計
算の高速化を図らなくてはならない。そこで、計算量を減らすことを考える。
位になるとこの式を計算するのにかなりの時間がかかり実用に適さない。実際、FFTを使
いたい場面ではリアルタイム(少なくとも1秒くらい)で計測が終わる必要があるので、計
算の高速化を図らなくてはならない。そこで、計算量を減らすことを考える。
そのために、![]() を整数、
を整数、![]() も整数であるがその範囲は
も整数であるがその範囲は
![]() とした場合の
とした場合の
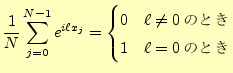 |
(7) |
を使う。この式の計算については、3.1節を見よ。さて、ここから が本題で、式(5)の両辺に
| (8) |
を乗じて、
となる。これで、
である。この式が離散フーリエ変換(DFT)と呼ばれるものである。もう少し分 かりやすく書くと、
である。
以上をまとめると、区間
![]() の場合の離散逆フーリエ変換が式
(4)、離散フーリエ変換が式(10)である。
の場合の離散逆フーリエ変換が式
(4)、離散フーリエ変換が式(10)である。
1.2 区間
![$ {\boldsymbol [0,T]}$](img51.png) の場合
の場合
これまでは区間
独立変数を ![]() として、区間でのデータの取得は
として、区間でのデータの取得は
| (12) |
とする。展開の基底を、
| (13) |
のように選ぶ。ここで、
| (14) |
と書き改められる。ここで、
基底の線形和として、元の関数![]() は、
は、
となる。これは、フーリエ逆変換である。今は離散データを問題としているので、
と書き表せる。この
である。式(16)の両辺に
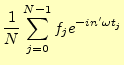 |
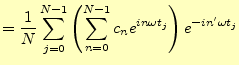 |
(18) |
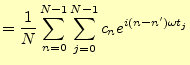 |
||
となる。従って、この場合の離散フーリエ変換は
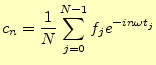 |
(19) |
となる。
1.3 まとめと実際の計算
これまで示した離散フーリエ変換の結果をまとめて、整理しておく。区間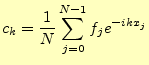 |
(20) | |||
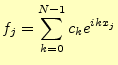 |
(21) |
である。区間
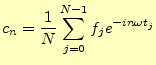 |
(22) | |||
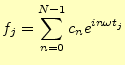 |
(23) |
である。ただし、
データが
![]() の場合の離散フーリエ変換
のプログラムを作成する式を示しておくのが良いだろう。そこで、区間
の場合の離散フーリエ変換
のプログラムを作成する式を示しておくのが良いだろう。そこで、区間 ![]() の
式を
の
式を
![]() と
と
![]() を使って、
を使って、
と書き改める。コンピューターで離散フーリエ変換を計算する場合は、これらの式を計算すべき である。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月29日