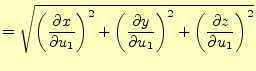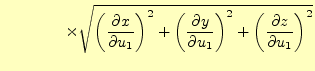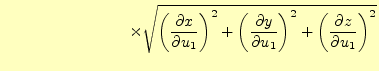座標系を変えた場合の空間での距離を考える。空間の非常に近い2点 を考える。それ
ぞれの点を、カーテシアン座標系では
を考える。それ
ぞれの点を、カーテシアン座標系では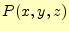 と
と
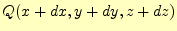 とする。すると、
2点間の距離
とする。すると、
2点間の距離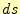 は
は
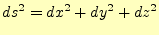 |
(21) |
となる。中学校以来おなじみの3平方の定理である。
それでは、これを一般化して、他の直交座標系でも成り立つのであろうか?。これは、成
り立つはずもなく、
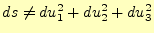 である。そこで、他の座標系の場合、
距離
である。そこで、他の座標系の場合、
距離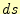 がどうなるか、もう少しまじめに考えよう。
がどうなるか、もう少しまじめに考えよう。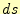 の2乗は、変位ベクトル
の2乗は、変位ベクトル
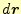 自身の内積に等しい。変位ベクトルは式(17)を使え
ば簡単に求められる。これらをまとめると
自身の内積に等しい。変位ベクトルは式(17)を使え
ば簡単に求められる。これらをまとめると
となる。この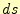 を線素という。
を線素という。
これは、これで正確であるが、こんな計算をするまでもなくスケール因子の役割をわかり
やすく記述する式(20)を使う方が良い。この方がストレー
トで憶えやすい。
直交曲面座標を使っているので簡単である。
カーテシアン座標系の面積素は、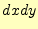 のように表される。
のように表される。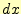 は、
は、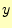 と
と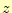 を固定して、
を固定して、
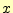 を微少変位させた長さである。同様に、
を微少変位させた長さである。同様に、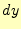 は、
は、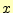 と
と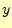 を固定して、
を固定して、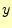 を微小変化
させたものである。この場合、
を微小変化
させたものである。この場合、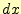 と
と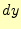 はお互いに直交しているので、それが作る長方
形の面積は、
はお互いに直交しているので、それが作る長方
形の面積は、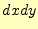 となる。これが面積素で、これを足しあわせる(積分)と、その面の面
積になる。ここでは、曲線座標でどのようになるか計算する。これは、後の微分演算子を
求めることに使われる。
となる。これが面積素で、これを足しあわせる(積分)と、その面の面
積になる。ここでは、曲線座標でどのようになるか計算する。これは、後の微分演算子を
求めることに使われる。
座標を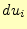 微少変位させた軌跡と、
微少変位させた軌跡と、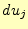 微少変位させた軌跡で作られる平行四辺形
5の面積
微少変位させた軌跡で作られる平行四辺形
5の面積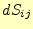 とする。その面積は、ベ
クトル積の絶対値として計算できるので
とする。その面積は、ベ
クトル積の絶対値として計算できるので
となる。これが曲線座標の面積素である。
なにも、ベクトル積を計算しないまでも、
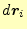 と
と
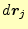 は直交することと、
それぞれの大きさは
は直交することと、
それぞれの大きさは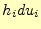 と
と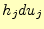 から、その面積は
から、その面積は
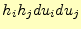 と直接計算
できる。ここでもスケール因子が便利であることがわかる。さらに、直交座標系を使うこと
の恩恵を被ることができる。
と直接計算
できる。ここでもスケール因子が便利であることがわかる。さらに、直交座標系を使うこと
の恩恵を被ることができる。
体積素も面積素と考え方はおなじである。従って、体積素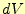 は
は
となる。これも、こんな計算をするまでもなく、直交座標系であることと、スケール因子
が理解できていれば、直感的に求めることができる。
体積素はこれで終わりであるが、ヤコビ行列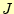 との関係を少し述べておく。座標変換を行っ
た場合の体積素は、
との関係を少し述べておく。座標変換を行っ
た場合の体積素は、
の関係がある。これと式(25)から、
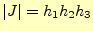 と推測ができる。しかし、式(26)の行ベクトルが直交して
いるという条件を使い、行列式を計算するのは大変やっかいである。そこで、行列式の見方を変え
ることにする。行列式の値は、その行ベクトルが作る平行6面体の体積に等しいはずであ
る。この場合、行ベクトルは直交しているので直方体になる。その体積は簡単で、それぞ
れのベクトルの大きさを乗算すればよい。従って、
と推測ができる。しかし、式(26)の行ベクトルが直交して
いるという条件を使い、行列式を計算するのは大変やっかいである。そこで、行列式の見方を変え
ることにする。行列式の値は、その行ベクトルが作る平行6面体の体積に等しいはずであ
る。この場合、行ベクトルは直交しているので直方体になる。その体積は簡単で、それぞ
れのベクトルの大きさを乗算すればよい。従って、
となるのは、明らかであろう。この式の右辺は、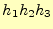 である。ヤコビ行列を使っ
ても同じ結果が得られるのである。
である。ヤコビ行列を使っ
ても同じ結果が得られるのである。
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成20年3月24日
![]() である。そこで、他の座標系の場合、
距離
である。そこで、他の座標系の場合、
距離![]() がどうなるか、もう少しまじめに考えよう。
がどうなるか、もう少しまじめに考えよう。![]() の2乗は、変位ベクトル
の2乗は、変位ベクトル
![]() 自身の内積に等しい。変位ベクトルは式(17)を使え
ば簡単に求められる。これらをまとめると
自身の内積に等しい。変位ベクトルは式(17)を使え
ば簡単に求められる。これらをまとめると
![]() 微少変位させた軌跡と、
微少変位させた軌跡と、![]() 微少変位させた軌跡で作られる平行四辺形
5の面積
微少変位させた軌跡で作られる平行四辺形
5の面積![]() とする。その面積は、ベ
クトル積の絶対値として計算できるので
とする。その面積は、ベ
クトル積の絶対値として計算できるので
![]() と
と
![]() は直交することと、
それぞれの大きさは
は直交することと、
それぞれの大きさは![]() と
と![]() から、その面積は
から、その面積は
![]() と直接計算
できる。ここでもスケール因子が便利であることがわかる。さらに、直交座標系を使うこと
の恩恵を被ることができる。
と直接計算
できる。ここでもスケール因子が便利であることがわかる。さらに、直交座標系を使うこと
の恩恵を被ることができる。
![]() との関係を少し述べておく。座標変換を行っ
た場合の体積素は、
との関係を少し述べておく。座標変換を行っ
た場合の体積素は、