電磁現象を記述する微分方程式は、マクスウェルの方程式と呼ばれ
と書かれる4組の連立の微分方程式である。ここで、
| 記号 |
物理量 |
単位 |
スカラー/ベクトル |
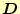 |
電束密度 |
[
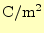 ] ] |
ベクトル |
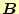 |
磁束密度 |
[T]あるは[
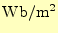 ] ] |
ベクトル |
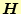 |
磁場(の強さ) |
[
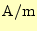 ] ] |
ベクトル |
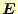 |
電場(の強さ) |
[
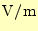 ] ] |
ベクトル |
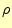 |
電荷密度 |
[
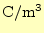 ] ] |
スカラー |
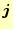 |
電流密度 |
[
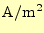 ] ] |
ベクトル |
である。物質中では、
という関係で結びつけられている。ここで、
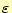 は誘電率、
は誘電率、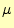 は透磁率、
は透磁率、
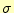 導電率である。これらの量は、一般
2には2階のテンソルになる。
ヘルムホルツ方程式は、楕円型の微分方程式で
導電率である。これらの量は、一般
2には2階のテンソルになる。
ヘルムホルツ方程式は、楕円型の微分方程式で
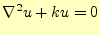 |
(8) |
の形のものを言う。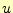 はベクトルの場合とスカラーの場合がある。ここでは、真空で何もない
空間の電磁場の方程式が、この形になることを示す。ようするに、マクスウェルの方程
式に何もない空間(真空)と言う条件を課して、ヘルムホルツ方程式を導くのである。
はベクトルの場合とスカラーの場合がある。ここでは、真空で何もない
空間の電磁場の方程式が、この形になることを示す。ようするに、マクスウェルの方程
式に何もない空間(真空)と言う条件を課して、ヘルムホルツ方程式を導くのである。
まずは、何もない真空の空間ではあるが、そこには電磁場は存在する。しかし、
電荷や電流は存在しないものとする。従って
となる。また、真空中では誘電率や透磁率は一定で、それらは
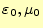 と
書き表すことにする。これら、真空中という条件をまとめると、マクスウェルの方程式は、
と
書き表すことにする。これら、真空中という条件をまとめると、マクスウェルの方程式は、
となる。これは、電場と磁場の連立微分方程式である。
これをそのまま計算するのは大変なので、電場、あるいは磁場のみの式に直す。そのため
に、式(14)の両辺に回転の演算子を作用させる。すると、
となる。この式の左辺はベクトル恒等式と式(13)を用いると
と変形できる。一方、式(16)の右辺は時間と空間の微分である回転を入
れ替え、式(15)を用いると、
となる。これら、左辺と右辺の結果の式(17),
(18)から、式(16)は
と書き直せる。これが、磁場を表す微分方程式である。この式は、空間の2回微分と時間
の2回微分の項が現れており、波動方程式になっている。この式は、何もない空間で時間
変化する電磁場は波になっていると言っているのである。波であれば、その速度があり、
この式から電磁場の伝搬速度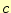 は、
は、
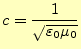 |
(20) |
が分かる。この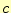 は光速を示し、電磁場の伝搬速度速度である。驚いたことに、誘電率
は光速を示し、電磁場の伝搬速度速度である。驚いたことに、誘電率
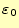 と透磁率
と透磁率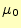 が光速と関係しているのである。
が光速と関係しているのである。
時間変化する波を解析する場合、周波数に分解して考えるのは常套手段である。ここでは、
それをフーリエ解析を用いて丁寧に示すことにする。ここの磁場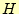 は、時間と空間の関
数である。そして、時間の関数は変数分離できることは直感的に理解できる。したがって、
磁場は
は、時間と空間の関
数である。そして、時間の関数は変数分離できることは直感的に理解できる。したがって、
磁場は
と書き表せるだろう。そして、この時間の項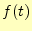 をフーリエ変換すると
をフーリエ変換すると
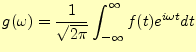 |
(22) |
となる。この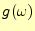 を用いて、フーリエ逆変換することにより、時間の項は
を用いて、フーリエ逆変換することにより、時間の項は
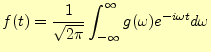 |
(23) |
と表せる。これで、式(19)をヘルムホルツ方程式に直す準備
は整った。
波動方程式(19)の磁場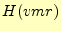 の項を変数分離して、その
時間の項をフーリエ解析で処理すれば、目的のヘルムホルツ方程式が得られる。まずは、
式(19)を式(21)を用いて、
変数分離すると、
の項を変数分離して、その
時間の項をフーリエ解析で処理すれば、目的のヘルムホルツ方程式が得られる。まずは、
式(19)を式(21)を用いて、
変数分離すると、
| |
![$\displaystyle \nabla^2\left[\boldsymbol{H}(\boldsymbol{r})f(t)\right]- \frac{1}...
...tial^{2} }{\partial t^{2}}\fi \left[\boldsymbol{H}(\boldsymbol{r})f(t)\right]=0$](img54.png) |
|
| |
時間と空間の微分を分けると |
|
| |
![$\displaystyle f(t)\nabla^2\left[\boldsymbol{H}(\boldsymbol{r})\right]- \boldsym...
...}{\partial t} \else \frac{\partial^{2} }{\partial t^{2}}\fi \left[f(t)\right]=0$](img55.png) |
(24) |
と書き表すことができる。この式に、フーリエ解析の式(23)を適用す
ると、
![$\displaystyle \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty}g(\omega)e^{-i\omega...
...{\infty}g(\omega)e^{-i\omega t}d\omega \boldsymbol{H}(\boldsymbol{r}) \right]=0$](img56.png) |
(25) |
となる。時間の2階微分は、
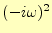 がでるため、
がでるため、
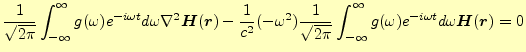 |
(26) |
と書き表せる。積分の項は同じなので、両辺をそれで割ると、
とヘルムホルツ方程式が得られる。ここで、この微分方程式の解である
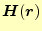 を固有関数、
を固有関数、
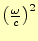 を固有値と言う。
を固有値と言う。
電場の場合も全く同様にして求められる。電場の場合は
となる。
ヘルムホルツ方程式は、時間の微分が入らないため、計算がきわめて簡単になる。この2
階の微分方程式を適当な境界条件を課して、解けば電磁場が分かる。これは、モードに分
けて計算しているので、時間の項は全て
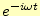 がかかることになる。この辺の
話は、また機会があるときにする。
がかかることになる。この辺の
話は、また機会があるときにする。
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年8月20日
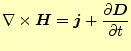
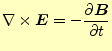
![]() は、時間と空間の関
数である。そして、時間の関数は変数分離できることは直感的に理解できる。したがって、
磁場は
は、時間と空間の関
数である。そして、時間の関数は変数分離できることは直感的に理解できる。したがって、
磁場は
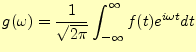
![]() の項を変数分離して、その
時間の項をフーリエ解析で処理すれば、目的のヘルムホルツ方程式が得られる。まずは、
式(19)を式(21)を用いて、
変数分離すると、
の項を変数分離して、その
時間の項をフーリエ解析で処理すれば、目的のヘルムホルツ方程式が得られる。まずは、
式(19)を式(21)を用いて、
変数分離すると、
![$\displaystyle \nabla^2\left[\boldsymbol{H}(\boldsymbol{r})f(t)\right]- \frac{1}...
...tial^{2} }{\partial t^{2}}\fi \left[\boldsymbol{H}(\boldsymbol{r})f(t)\right]=0$](img54.png)
![$\displaystyle f(t)\nabla^2\left[\boldsymbol{H}(\boldsymbol{r})\right]- \boldsym...
...}{\partial t} \else \frac{\partial^{2} }{\partial t^{2}}\fi \left[f(t)\right]=0$](img55.png)
![$\displaystyle \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty}g(\omega)e^{-i\omega...
...{\infty}g(\omega)e^{-i\omega t}d\omega \boldsymbol{H}(\boldsymbol{r}) \right]=0$](img56.png)
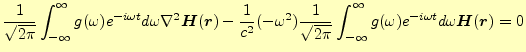
![]() がかかることになる。この辺の
話は、また機会があるときにする。
がかかることになる。この辺の
話は、また機会があるときにする。