FDTD法で計算すべき式は,式(6)と式(7)
を評価することにより得られる.これは,図1の構
造を形作っている多数の立体,これを体積素と言うことにして,それらを個別に積分する
ことにより求められる.
この体積素を構成する平面,これを面積素ということにして,このうちの一つrz平面で式
(6)を評価してみよう.体積素が小さいとして,この式の左辺
は電場の線績分を表し,図4に示すように経路では,
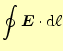 |
$](img50.png) |
(14) |
と近似ができる.右辺の方の近似は,
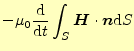 |
(r_{j+1/2}-r_{j-1/2})$](img52.png) |
(15) |
となる.この両辺は等しいので,
となる.これから,
![$\displaystyle H_{\theta\;i,j}^{\mspace{12mu}n+1}\simeq H_{\theta\;i,j}^{\mspace...
...{12mu}n+1/2}-E_{z\;i,j-1/2}^{\mspace{12mu}n+1/2}} {r_{j+1/2}-r_{j-1/2}} \right]$](img54.png) |
(16) |
が得られる.この式の右辺は,時刻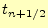 の電場
の電場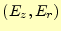 と
と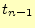 の磁場
の磁場
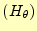 である.左辺は,時刻
である.左辺は,時刻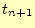 の磁場
の磁場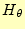 である.
である.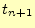 の磁場
は,それ以前の情報があれば計算できると言っているのである.
の磁場
は,それ以前の情報があれば計算できると言っているのである.
図 4:
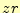 平面の積分路
平面の積分路
|
|
次に,先ほどと同様のことを図5の領域について行う.ここで
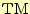 モードについて計算しているので,
モードについて計算しているので,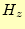 が無いことに注意して積分を行う.
式(7)の左辺の積分は,
が無いことに注意して積分を行う.
式(7)の左辺の積分は,
![$\displaystyle \oint{\boldsymbol{H}}\cdot\mathrm{d}\ell \simeq\left[ H_{\theta\;i-1,j}^{\mspace{12mu}n}-H_{\theta\;i,j}^{\mspace{12mu}n} \right]r_j\Delta\theta$](img68.png) |
(17) |
となる.
式(7)の右辺の積分は,
r_j\Delta\theta$](img69.png) |
(18) |
となる.両辺は等しいので,
$](img70.png) |
(19) |
である.これから,電場の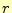 方向成分を求める式
方向成分を求める式
![$\displaystyle E_{r\;i-1/2,j}^{\mspace{12mu}n+1/2} \simeq E_{r\;i-1/2,j}^{\mspac...
...ft[ H_{\theta\;i-1,j}^{\mspace{12mu}n}-H_{\theta\;i,j}^{\mspace{12mu}n} \right]$](img72.png) |
(20) |
が得られる.先ほど同様,これも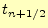 の電場
の電場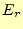 は,それ以前の電磁場から求
められると言っている.
は,それ以前の電磁場から求
められると言っている.
図 5:
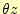 平面の積分路
平面の積分路
|
|
最後に,いままでと同様のことを図6の領域について行う.ここで
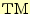 モードについて計算しているので,
モードについて計算しているので,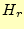 が無いことに注意して積分を行う.
式(7)の左辺の積分は,
が無いことに注意して積分を行う.
式(7)の左辺の積分は,
![$\displaystyle \oint{\boldsymbol{H}}\cdot\mathrm{d}\ell \simeq \left[ H_{\theta\...
...{\mspace{12mu}n}r_{j+1}-H_{\theta\;i,j}^{\mspace{12mu}n}r_j \right]\Delta\theta$](img81.png) |
(21) |
となる.
式(7)の右辺の積分は,
![$\displaystyle \varepsilon_0\frac{\mathrm{d}}{\mathrm{d}t}\int_S\boldsymbol{E}\c...
...\;i,j+1/2}^{\mspace{12mu}n-1/2} \right]\frac{1}{2}(r_{j+1}^2-r_j^2)\Delta\theta$](img82.png) |
(22) |
となる.両辺は等しいので,
$](img83.png) |
(23) |
となる.これから,電場の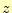 方向成分を求める式
方向成分を求める式
が得られる.いままで同様,これも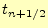 の電場
の電場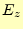 は,それ以前の電磁場から求
められると言っている.
は,それ以前の電磁場から求
められると言っている.
図 6:
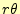 平面の積分路
平面の積分路
|
|
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年8月20日
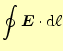
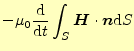
(r_{j+1/2}-r_{j-1/2})
\end{multline}](img53.png)
![$\displaystyle H_{\theta\;i,j}^{\mspace{12mu}n+1}\simeq H_{\theta\;i,j}^{\mspace...
...{12mu}n+1/2}-E_{z\;i,j-1/2}^{\mspace{12mu}n+1/2}} {r_{j+1/2}-r_{j-1/2}} \right]$](img54.png)
![$\displaystyle \oint{\boldsymbol{H}}\cdot\mathrm{d}\ell \simeq\left[ H_{\theta\;i-1,j}^{\mspace{12mu}n}-H_{\theta\;i,j}^{\mspace{12mu}n} \right]r_j\Delta\theta$](img68.png)
r_j\Delta\theta$](img69.png)
![$\displaystyle E_{r\;i-1/2,j}^{\mspace{12mu}n+1/2} \simeq E_{r\;i-1/2,j}^{\mspac...
...ft[ H_{\theta\;i-1,j}^{\mspace{12mu}n}-H_{\theta\;i,j}^{\mspace{12mu}n} \right]$](img72.png)
![$\displaystyle \oint{\boldsymbol{H}}\cdot\mathrm{d}\ell \simeq \left[ H_{\theta\...
...{\mspace{12mu}n}r_{j+1}-H_{\theta\;i,j}^{\mspace{12mu}n}r_j \right]\Delta\theta$](img81.png)
![$\displaystyle \varepsilon_0\frac{\mathrm{d}}{\mathrm{d}t}\int_S\boldsymbol{E}\c...
...\;i,j+1/2}^{\mspace{12mu}n-1/2} \right]\frac{1}{2}(r_{j+1}^2-r_j^2)\Delta\theta$](img82.png)
![$\displaystyle \simeq E_{z\;i,j+1/2}^{\mspace{12mu}n-1/2}+ \frac{2(t_{n+1/2}-t_{...
...eta\;i,j+1}^{\mspace{12mu}n}r_{j+1}-H_{\theta\;i,j}^{\mspace{12mu}n}r_j \right]$](img86.png)
![$\displaystyle \simeq E_{z\;i,j+1/2}^{\mspace{12mu}n-1/2}+ \frac{2(t_{n+1/2}-t_{...
...eta\;i,j+1}^{\mspace{12mu}n}r_{j+1}-H_{\theta\;i,j}^{\mspace{12mu}n}r_j \right]$](img87.png)