平成16年度横浜国立大学工学部編入試験に出題された問題である。
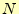 個の要素を持つ整数型配列a[]が与えられているとする。このとき、a[0]〜
a[N-1]の要素を昇順に整列するプログラムについて以下の問いに答えなさい。
個の要素を持つ整数型配列a[]が与えられているとする。このとき、a[0]〜
a[N-1]の要素を昇順に整列するプログラムについて以下の問いに答えなさい。
なお、/*1*/の行の割算は整数の割算(小数点以下切捨て)である。
- [問1]
- 下記プログラムが目標どおり動作するように
![\framebox[5mm][c]{\hspace{3mm}{{\footnotesize A}}\hspace{3mm}}](img16.png) 〜
〜
![\framebox[5mm][c]{\hspace{3mm}{{\footnotesize D}}\hspace{3mm}}](img17.png) を埋めな
さい。ただし、下記プログラムにおいてNの値は8である。
を埋めな
さい。ただし、下記プログラムにおいてNの値は8である。
- [問2]
- 完成したプログラムの出力結果を示しなさい。ただし、複数行の出力が印
刷される場合には、各行の時間順序も正しくないといけません。
- [問3]
- このアルゴリズムでは配列a[]の要素の比較回数(/*2*/および
/*3*/の関係演算子の実行回数)は、一般にどれくらいと見積もられる
か。
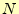 を用いた式を用いて簡潔に説明しなさい。
を用いた式を用いて簡潔に説明しなさい。
#include <stdio.h>
#define N 8
int a[N]={3,1,5,8,2,6,7,4};
void sort(int [], int, int);
void swap(int [], int, int);
void main(void){
sort(a, 0, N-1);
}
void sort(int a[], int L, int R){
int i, j, part;
i = L;
j = R;
part = a[(L+R)/2];
do{
while(a[i] < part) i++;
while(part < a[j]) j--;
if(i <= j){
swap(a, i, j);
i++;
j--;
}
}while(i <= j);
if(L < j)sort(a,
![\framebox[5mm][c]{\hspace{3mm}{{\footnotesize A}}\hspace{3mm}}](img19.png)
,
![\framebox[5mm][c]{\hspace{3mm}{{\footnotesize B}}\hspace{3mm}}](img20.png)
);
if(i < R)sort(a,
![\framebox[5mm][c]{\hspace{3mm}{{\footnotesize C}}\hspace{3mm}}](img21.png)
,
![\framebox[5mm][c]{\hspace{3mm}{{\footnotesize D}}\hspace{3mm}}](img22.png)
);
}
void swap(int a[], int x, int y){
int temp;
temp = a[x];
a[x] = a[y];
a[y] = temp;
printf("(%d, %d)\n", x, y);
}
クイックソートに関する出題である。クイックソートが理解できていれば解ける
はずである。問3は少し難しく、一度学習していないと解けないだろう。それでは、解答
を以下に示す。
- [問1]
- クイックソートのプログラムにするためには、A〜Dは以下の通りにする必
要がある。
![\framebox[5mm][c]{\hspace{3mm}{{\footnotesize A}}\hspace{3mm}}](img23.png) L
L
![\framebox[5mm][c]{\hspace{3mm}{{\footnotesize B}}\hspace{3mm}}](img24.png) j
j
![\framebox[5mm][c]{\hspace{3mm}{{\footnotesize C}}\hspace{3mm}}](img25.png) i
i
![\framebox[5mm][c]{\hspace{3mm}{{\footnotesize D}}\hspace{3mm}}](img26.png) R
R
- [問2]
- プログラムの出力は以下の通り。
(3, 7)
(2, 4)
(3, 3)
(0, 1)
(1, 2)
(5, 5)
- [問3]
- sort()関数が最初に呼び出されたときの比較(/*2*/と
/*3*/)の実行回数は、
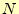 あるいは
あるいは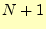 回である。平均で、
回である。平均で、
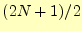 回の比較が行われる。そして、再帰呼び出しにより、
回の比較が行われる。そして、再帰呼び出しにより、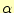 個と
個と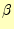 個の場合のsort()が呼び出されることになる。
個の場合のsort()が呼び出されることになる。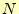 個の時
のトータルの比較回数を
個の時
のトータルの比較回数を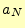 として、これらの関係は、
として、これらの関係は、
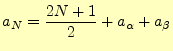 |
(1) |
となる。もちろん、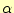 と
と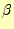 は、
は、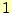 〜
〜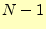 の値を取りうる。そ
して、a[]に格納されている値がランダムであれば、同
じ確率で
の値を取りうる。そ
して、a[]に格納されている値がランダムであれば、同
じ確率で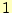 〜
〜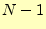 の値をとる。さらに、
の値をとる。さらに、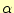 と
と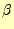 の和は
の和は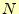 に
なることはクイックソートのアルゴリズムから自明である。したがって、
に
なることはクイックソートのアルゴリズムから自明である。したがって、
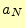 の期待値は、
の期待値は、
となる。この漸化式から、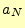 を求めることになるが、計算は結構大変で
ある。まず、式(2)を
を求めることになるが、計算は結構大変で
ある。まず、式(2)を
と変形しておく。つぎに、この式の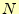 を
を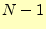 にした場合の式
にした場合の式
を利用する。式(3)から式(4)の辺々を差
し引いて整理すると、
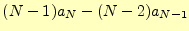 |
![$\displaystyle = \frac{1}{2}\left[(2N+1)(N-1)-(2N-1)(N-2)\right]+2a_{N-1}$](img54.png) |
(5) |
となる。さらに、整理を進めると
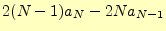 |
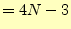 |
(6) |
となる。両辺を、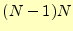 で割ると、
で割ると、
となる。ここで、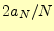 を
を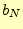 と置くと、
と置くと、
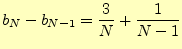 |
(8) |
となり、階差数列を用いて容易に計算できる。すなわち、
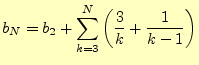 |
(9) |
である。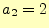 より、
より、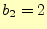 となるので、
となるので、
となる。ここで、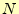 が大きい場合、
が大きい場合、
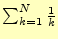 は
は
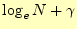 に近づくことが知られている2。
に近づくことが知られている2。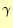 はオイラー数と言われる定数で、その値は
0.577
はオイラー数と言われる定数で、その値は
0.577 である。したがって、
である。したがって、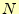 が大きい場合、
が大きい場合、
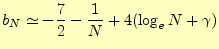 |
(11) |
となる。右辺の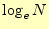 は他の項に比べて大きな値を取る3。したがっ
て、
は他の項に比べて大きな値を取る3。したがっ
て、
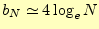 |
(12) |
となる。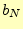 の定義から、
の定義から、
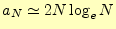 |
(13) |
となる。
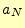 はa[]の要素の比較回数を表す。したがって、
はa[]の要素の比較回数を表す。したがって、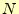 が大
きい場合の比較回数は、
が大
きい場合の比較回数は、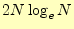 となる。
となる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年8月22日
![\framebox[5mm][c]{\hspace{3mm}{{\footnotesize A}}\hspace{3mm}}](img19.png)
![\framebox[5mm][c]{\hspace{3mm}{{\footnotesize B}}\hspace{3mm}}](img20.png)
![\framebox[5mm][c]{\hspace{3mm}{{\footnotesize C}}\hspace{3mm}}](img21.png)
![\framebox[5mm][c]{\hspace{3mm}{{\footnotesize D}}\hspace{3mm}}](img22.png)
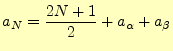
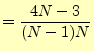
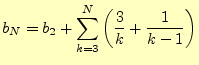
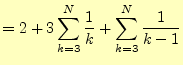
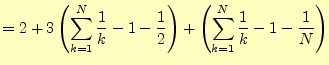
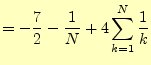
![]() はa[]の要素の比較回数を表す。したがって、
はa[]の要素の比較回数を表す。したがって、![]() が大
きい場合の比較回数は、
が大
きい場合の比較回数は、![]() となる。
となる。