3次元のスカラー場を図にすることは大変なので,最初は2次元スカラー場を用いて説明す
る.ただ,3次元でも全く同じことであることは頭の隅に入れておく必要がある.2次元の
スカラー場として,山の高さ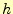 を考える.これは,位置ベクトル
を考える.これは,位置ベクトル
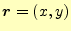 の関数
で
の関数
で
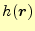 あるいは
あるいは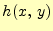 と書くことができる.
と書くことができる.
ここで,
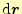 だけ異なる位置の山の高さの差
だけ異なる位置の山の高さの差
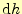 を考える.これは,
を考える.これは,
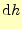 |
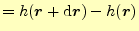 |
|
| |
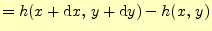 |
|
| |
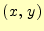 の周りでテーラー展開して,1次の項のみをとると の周りでテーラー展開して,1次の項のみをとると |
|
| |
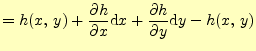 |
|
| |
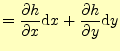 |
(7) |
となる.最後の式は全微分の式そのものなので,いきなりこれを書いても良い.ここでは,
山の高さの差が分かりやすいように,テーラー展開を用いて示しただけである.ところで
この式は,
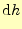 |
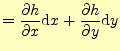 |
|
| |
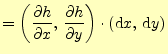 |
|
| |
![$\displaystyle =\left[\left( \if 11 \frac{\partial }{\partial x} \else \frac{\pa...
...rtial^{1} }{\partial y^{1}}\fi \right)h\right] \cdot(\mathrm{d}x,\,\mathrm{d}y)$](img34.png) |
|
| |
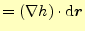 |
|
| |
括弧が無くても微分の順序は間違うことはないので |
|
| |
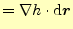 |
(8) |
と書くことができるであろう.最後の式がベクトルで表した山の高さの差である.先週示したように,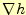 は
は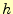 の勾配と呼ばれるベクトル量である.むろん,変位
の勾配と呼ばれるベクトル量である.むろん,変位
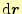 はベクトル量である.そしてこれらのベクトル量のスカラー積は,2点間の山の
高さの差
はベクトル量である.そしてこれらのベクトル量のスカラー積は,2点間の山の
高さの差
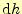 を表し,それは明らかにスカラー量となる.山を歩いていて,
を表し,それは明らかにスカラー量となる.山を歩いていて,
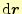 移動すると,
移動すると,
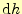 標高が変化するということを表している.ただし,式
(8)は,
標高が変化するということを表している.ただし,式
(8)は,
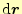 がゼロの極限のみで正しいことを忘れて
はならない.
がゼロの極限のみで正しいことを忘れて
はならない.
ここで勾配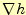 の意味を考えなくてはならない.勾配
の意味を考えなくてはならない.勾配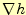 はベクトル量なの
で方向と大きさを持っているはずである.方向はどっちを向いているのか?その大きさは?--
ということである.それを考えるために,式(8)を
はベクトル量なの
で方向と大きさを持っているはずである.方向はどっちを向いているのか?その大きさは?--
ということである.それを考えるために,式(8)を
と書き換える.もちろん,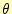 は2つのベクトルの間の角度である.勾配は場の量と
して決まっているが,変位
は2つのベクトルの間の角度である.勾配は場の量と
して決まっているが,変位
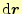 は任意にとれる.地形は変えられないが,そこ
を歩く人間はどの方向にも向かうことができる.ぐるっと見渡して,いろいろな方向に歩
いてみる.同じだけ歩いてもっとも高く登れるのは,2つのベクトルが同じ方向を向いて
いる場合である.式(9)から,当然である.このことか
ら,勾配はスカラー場の変化が最も大きい方向に向かっているのである.具体的には,一
歩を踏み出したとき,最も坂道のきつい方向が勾配
は任意にとれる.地形は変えられないが,そこ
を歩く人間はどの方向にも向かうことができる.ぐるっと見渡して,いろいろな方向に歩
いてみる.同じだけ歩いてもっとも高く登れるのは,2つのベクトルが同じ方向を向いて
いる場合である.式(9)から,当然である.このことか
ら,勾配はスカラー場の変化が最も大きい方向に向かっているのである.具体的には,一
歩を踏み出したとき,最も坂道のきつい方向が勾配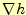 の方向である.
の方向である.
スカラー場を等高線で表すと勾配はそれと直角方向にスカラー場の値が大きくなる方向に
向かってる.なぜならば,その方向が最も高さ変化が大きい方向となっているからである.
式(9)から,勾配の大きさはスカラー場の変化の割合を
表していることがわかる.高さの変化の割合--山の傾斜--が勾配の大きさである.した
がって,等高線の密度が詰まっているときに勾配は大きくなる.数学用語で勾配と言って
いるが,坂道を上るときの勾配と同じ--ということが理解できるであろう.スカラー場
の微分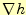 を勾配と言うのは,わかりやすい良い名前である.
を勾配と言うのは,わかりやすい良い名前である.
ここでは2次元で話を進めたが,3次元スカラー場でも全く同じである.3次元の場合は,
等高線ではなく等高面になる.この場合の勾配は,等高面に垂直で,スカラー場の値が大
きくなる方向に向かっている.スカラー場の大きさは,等高面の間隔反比例しているのは
2次元の場合と同じである.4次元の場合はどうなるか?.これは絵ではかけないので,式
で考えるしかない.ただし,同じ形をしている.
式(6)のように,微分したものの積分を考える.勾配を積分したらど
うなるか--である.後で示すが,これは有用な面白い結果が得られる.それに対して,
スカラー場,そのものの積分はつまらない.必要になったとき,勝手に計算すればよい.
スカラー場の勾配の積分を考えるために,2つの場所
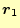 と
と
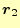 の標高差を
計算してみる.結論を先に言うと,これは勾配の積分として
の標高差を
計算してみる.結論を先に言うと,これは勾配の積分として
のように表すことができる.これは,正しそうであることが直感的にわかる.なぜならば,
これは高さの変化
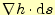 を足しあわせている式となっているから
である.
を足しあわせている式となっているから
である.
本当に正しいか?.標高差が
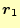 から
から
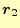 への経路に依存しないで,勾
配の積分で表せることを確かめなくてはならない.これが確かめられると,勾配の積分の
意味は,標高差を表すことがただちにわかる.
への経路に依存しないで,勾
配の積分で表せることを確かめなくてはならない.これが確かめられると,勾配の積分の
意味は,標高差を表すことがただちにわかる.
正しいことを確かめるために,ここでちょっとこの積分の意味を考えよう.積分の復習に
もなるので丁度良い教材である.元々積分は,値とその微少量をかけて足しあわせる演算
であった.次の式のようにである.
これは,ちょうど図3のように表せる.積分のパスを分割して,それ
ぞれの場所での勾配と変位の内積を計算して足しあわせる.そして,変位を無限小にした
場合の和が積分である.
次に,式(11)の和を考える.微少量の内積を図4に示す.こ
れは,式(8)から,
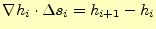 |
(12) |
となる.積分路を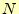 分割したとして,それを足しあわせると,
分割したとして,それを足しあわせると,
となる.ここで,
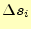 をゼロに近づけた極限では,
をゼロに近づけた極限では,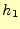 は
は
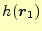 で,
で,
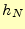 は
は
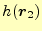 である.従って,式(10)が証明できた.これ
までの議論から,積分路に依存しないことも明らかであろう.
である.従って,式(10)が証明できた.これ
までの議論から,積分路に依存しないことも明らかであろう.
これも2次元で考えたが,3次元に拡張しても一般的に成り立つ.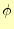 を3次元のスカラー
場とすると,
を3次元のスカラー
場とすると,
である.スカラー場の差は,勾配を積分すれば得られるのである.
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年10月10日
![]() だけ異なる位置の山の高さの差
だけ異なる位置の山の高さの差
![]() を考える.これは,
を考える.これは,
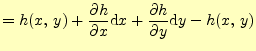
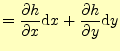
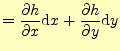
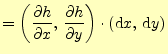
![$\displaystyle =\left[\left( \if 11 \frac{\partial }{\partial x} \else \frac{\pa...
...rtial^{1} }{\partial y^{1}}\fi \right)h\right] \cdot(\mathrm{d}x,\,\mathrm{d}y)$](img34.png)
![]() の意味を考えなくてはならない.勾配
の意味を考えなくてはならない.勾配![]() はベクトル量なの
で方向と大きさを持っているはずである.方向はどっちを向いているのか?その大きさは?--
ということである.それを考えるために,式(8)を
はベクトル量なの
で方向と大きさを持っているはずである.方向はどっちを向いているのか?その大きさは?--
ということである.それを考えるために,式(8)を
![]() を勾配と言うのは,わかりやすい良い名前である.
を勾配と言うのは,わかりやすい良い名前である.
![]() と
と
![]() の標高差を
計算してみる.結論を先に言うと,これは勾配の積分として
の標高差を
計算してみる.結論を先に言うと,これは勾配の積分として
![]() から
から
![]() への経路に依存しないで,勾
配の積分で表せることを確かめなくてはならない.これが確かめられると,勾配の積分の
意味は,標高差を表すことがただちにわかる.
への経路に依存しないで,勾
配の積分で表せることを確かめなくてはならない.これが確かめられると,勾配の積分の
意味は,標高差を表すことがただちにわかる.
![]() を3次元のスカラー
場とすると,
を3次元のスカラー
場とすると,