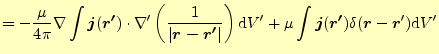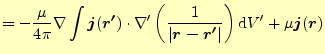3 静磁場の基本法則
3.1 ビオ・サバールの法則
式(5)は,無限に長い電流が作る磁場である.これが 分かると,微小な長さ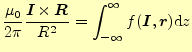 |
(6) |
となる
| (7) |
となる.ここまでくれば,
![]() がベクトルなので,
がベクトルなので,
![]() もベクトルになる必要がある.幸いな
ことに,磁場
もベクトルになる必要がある.幸いな
ことに,磁場![]() は電流
は電流
![]() とも位置
とも位置
![]() にも垂直である.そこで,微小磁場
にも垂直である.そこで,微小磁場
![]() は,ベクトル積
は,ベクトル積
![]() に関係がある--と類推できる.また,遠
距離
に関係がある--と類推できる.また,遠
距離![]() が離れると,磁場が小さくなることも理解できるであろう.問題は距離の何乗で
小さくなるか?--である.ここでは,距離の2乗としてみよう.間違っていれば,1乗に
したり,3乗にしてみて,正しい関数形を探せばよい.科学史に名前を残すことを考える
と,これくらいの努力をしてもよいだろう.これまでの直感から,
が離れると,磁場が小さくなることも理解できるであろう.問題は距離の何乗で
小さくなるか?--である.ここでは,距離の2乗としてみよう.間違っていれば,1乗に
したり,3乗にしてみて,正しい関数形を探せばよい.科学史に名前を残すことを考える
と,これくらいの努力をしてもよいだろう.これまでの直感から,
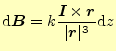 |
(8) |
とかける.比例定数の
この式を地道に積分を行う.計算する積分は
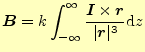 |
(9) |
である.ベクトルの積分となっており,通常はやっかいである.しかし,幸いなことに,
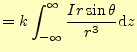 |
||
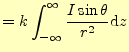 |
||
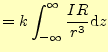 |
||
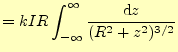 |
||
![$\displaystyle =kIR\left[\frac{z}{R^2\sqrt{R^2+z^2}}\right]_{-\infty}^\infty$](img55.png) |
||
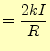 |
(10) |
この結果と式(5)を比べる.先の述べたように方向 は合っている.また,係数
| (11) |
とすれば,大きさも合う.したがって,微小領域
と考えても良い.普通,これをビオ-サバールの法則と言う.また,
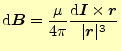 |
(13) |
と書かれる場合もある.
3.2 ベクトルポテンシャル
式(12)は,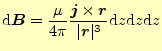 |
(14) |
と書き表すことができる.ここで,
これから,磁場を観測する位置ベクトルを
![]() とした場合の磁場は,
とした場合の磁場は,
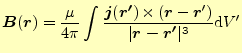 |
(15) |
となる.これが磁場を表す方程式の全てである.これは,
と書き表すことができる.なぜならば,
![$\displaystyle =-\frac{(x-x^\prime,y-y^\prime,z-z^\prime)} {\left[(x-x^\prime)^2+(y-y^\prime)^2+(z-z^\prime)^2\right]^{3/2}}\times\boldsymbol{c}$](img76.png) |
||
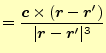 |
(17) |
が成り立つからである.
式(16)は,
| (18) |
と書くことができる.ただし,
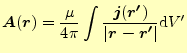 |
(19) |
である.この
3.3 磁場を表す微分方程式
この式から磁場を表す微分方程式を求める.ベクトル場を表す微分方程式は,発散と回転 である.先の磁場を表す方程式に発散と回転の演算を行えばよい.この辺の話は,文 献 [1]を参考にした.式(16)から,直ちに,
| (20) |
が求められる.なぜならば,回転の発散は恒等的にゼロとなるからである.
つぎに回転をもとめる.この場合,任意のベクトル場
![]() に関しての恒等式
に関しての恒等式
![]() を使う.式式
(16)の両辺に回転の演算を施すと,
を使う.式式
(16)の両辺に回転の演算を施すと,
![$\displaystyle =\nabla\times \nabla\times \left[\frac{\mu}{4\pi} \int\frac{\bold...
...dsymbol{r^\prime})}{\vert\boldsymbol{r-r^\prime}\vert}\mathrm{d}V^\prime\right]$](img86.png) |
(21) | |
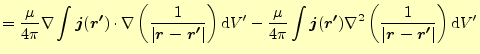 |
ここで,
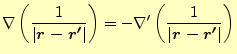 |
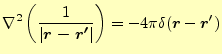 |
(22) |
を使う.これらの式については,第5回の講義ノートを見よ.これらを使うと,
が得られる.
この式の右辺第一項を計算するために,任意のベクトル場![]() と任意のスカラー場
と任意のスカラー場![]() の積
の発散を考える.それは,
の積
の発散を考える.それは,
| (24) |
となる.これを少しばかり変形すると
が得られる.式(23)のように微分が含まれる積分を行うときの定石であ る.部分積分である.
![$\displaystyle =\frac{\mu}{4\pi}\left[ \nabla\int\left(\frac{1}{\vert\boldsymbol...
...ime}\vert}\right)}\mathrm{d}V^\prime \right] +\mu\boldsymbol{j}(\boldsymbol{r})$](img98.png) |
(26) |
となる.このうち,左辺の第一項はゼロとなる.なぜならば,電荷保存則より静電場ではいつでも
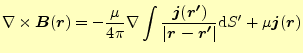 |
(27) |
が得られる.右辺第一項の積分は,全空間,すなわち宇宙全体にわたっての面積分である. 宇宙の端には電流が無い,あるいは電流密度が
| (28) |
となる.電流密度は,磁場の回転(の密度)を作るのである.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年7月25日
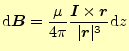
![\includegraphics[keepaspectratio,scale=1.0]{figure/Biot_Savart_line.eps}](img65.png)
![$\displaystyle \boldsymbol{B}(\boldsymbol{r})=\nabla\times \left[\frac{\mu}{4\pi...
...dsymbol{r^\prime})}{\vert\boldsymbol{r-r^\prime}\vert}\mathrm{d}V^\prime\right]$](img71.png)