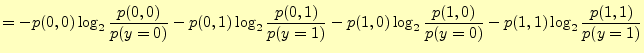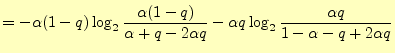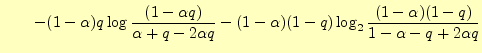図1のような状況を考える.送信者はメッセージ2を送り,
受信者はそれを受け取る.通信路の途中に雑音源があり,メッセージが変わることがある.
こういうことは,結構頻繁に生じる.遠距離の通信,例えば宇宙探査船が惑星の画像を送
る場合,かなりの確率で誤りが生じる.微弱な電波で長距離を伝送するからである.これほど
のことはないが,地上内の通信でも誤りの発生確率をゼロにすることはできない.熱雑音
を避けることはできないからである.宇宙線が問題になることもある.
図 1:
誤りのある通信の例.糸電話で通
信しているが,途中ノイズで波が鍋になっている.
|
|
これから,誤りのある通信路の理論的な考察を行う.ある程度の式を使うことになるが,
意味さえ分かれば難しいことは何もない.
送信者は,メッセージ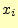 を送る.もし,アルファベット26文字のいずれかを送るなら
ば,
を送る.もし,アルファベット26文字のいずれかを送るなら
ば,
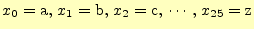 と考える.また,0か1のバイナリーデータを送るならば,
と考える.また,0か1のバイナリーデータを送るならば,
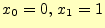 である.ここで,送信者が文字
である.ここで,送信者が文字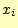 を送る確率を
を送る確率を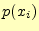 とする.すると,
とする.すると,
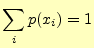 |
(1) |
である.送信者は,いずれかの文字を送るので,各々の確率を加えると1になるだけであ
る.
メッセージを受け取る受信者の方も同じで,受け取る文字を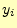 とする.ここでは,受
け取る文字の確率を
とする.ここでは,受
け取る文字の確率を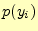 とする.もちろん,いずれかの文字を受け取るので,その和
は1になる.
とする.もちろん,いずれかの文字を受け取るので,その和
は1になる.
ここで,文字数が多くなると議論が複雑になるので,もっとも単純な二元対称通信路
(binary symeetric chanel)を考える.これは,図2
のような通信路で以下のように特徴づけられる.
- 通信に使う文字は
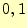 の2種類である.送信者は,これらの文字のみが送信で
きる.受信者は,こらの文字のみを受け取る.これが,二元対称通信路の「二元」という
ことを表している.
の2種類である.送信者は,これらの文字のみが送信で
きる.受信者は,こらの文字のみを受け取る.これが,二元対称通信路の「二元」という
ことを表している.
- 途中で誤りが発生する確率
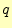 は,
は,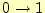 も
も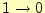 も同じである.この場合,
誤りが発生しない;
も同じである.この場合,
誤りが発生しない;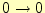 あるいは
あるいは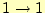 で正しく通信できる確率は
で正しく通信できる確率は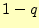 と
なる.これが,二元対称通信路の「対称」ということを表している.
と
なる.これが,二元対称通信路の「対称」ということを表している.
いつでもこのような状況が生じるわけではなく,このような理想的な状況を考える--と
いうことを理解しておく必要がある.例えば,'0'あるいは'1'という文字を送ったが,そ
れが途中で失われて,受信者には何も届かないこともある.また,'0'を送るときは
90[%]正しく通信ができるが,'1'を送るときには30[%]しか正しく通信できないことも
ある.これは対称ではない.
図 2:
二元対称性通信路.送信者,受信
者とも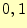 の符号を使う.通信途中で誤りが生じ,符号が入れ替わることがある.
通信途中で誤りが生じる確率は
の符号を使う.通信途中で誤りが生じ,符号が入れ替わることがある.
通信途中で誤りが生じる確率は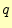 ,正しく通信ができる確率
,正しく通信ができる確率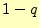 である.
である.
|
|
この2元対称通信路の場合,もっとも「質の悪い」エラーとはどのようなものだろうか?
100[%]の確率(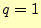 )で,エラーが起きる場合か? この場合,送られるメッセージと受け取るメッ
セージは,
)で,エラーが起きる場合か? この場合,送られるメッセージと受け取るメッ
セージは,
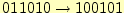 のようになる.受信者は,受け取ったメッセージから送っ
たメッセージが分かる.'0'と'1'を反転させれば良い.エラーが0[%]の時と同じだけ情
報を受け取ることができる.もっとも「質の悪い」エラーは50[%]の確率(
のようになる.受信者は,受け取ったメッセージから送っ
たメッセージが分かる.'0'と'1'を反転させれば良い.エラーが0[%]の時と同じだけ情
報を受け取ることができる.もっとも「質の悪い」エラーは50[%]の確率(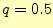 )でエラーが発生
する場合である.この場合,受け取るメッセージはランダムに'0'と'1'が並んだ数列に
なり,送信者の送った情報を全く受け取ることができない3.
)でエラーが発生
する場合である.この場合,受け取るメッセージはランダムに'0'と'1'が並んだ数列に
なり,送信者の送った情報を全く受け取ることができない3.
これから,誤りがある通信路の理論的な考察を行う.そのために,図
3に示すシステムを考える.このシステムは,送信者 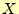 がある
文字
がある
文字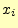 を送ると,受信者は
を送ると,受信者は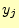 を受け取る.途中,信号にノイズが入り,メッセージ
が変化する可能性がある.それぞれの確率(probability)を以下のように定義する.
を受け取る.途中,信号にノイズが入り,メッセージ
が変化する可能性がある.それぞれの確率(probability)を以下のように定義する.
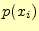 送信者が文字
送信者が文字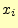 を送信する確率.
を送信する確率.
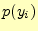 受信者が文字
受信者が文字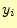 を受け取る確率.
を受け取る確率.
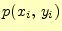 送信者が
送信者が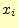 を送り,受信者が
を送り,受信者が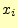 を受け取る確率.
を受け取る確率.
注意 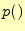 は関数ではない.また,添え字の
は関数ではない.また,添え字の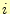 や
や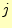 は送信/受信順序を表す
ものではない.
は送信/受信順序を表す
ものではない.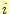 と
と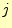 は文字の区別を行っている.
は文字の区別を行っている.
言うまでもないと思うが,全ての確率を加えると1になる.したがって,先ほど示したそれぞれ
の確率は
となる.また,
という関係も直ちに分かる.
図 3:
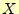 から
から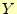 へメッセージを送る場合の確率.
へメッセージを送る場合の確率.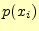 は送信者が
は送信者が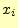 を送る
確率.
を送る
確率.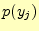 は受信者が
は受信者が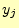 を受け取る確率.
を受け取る確率.
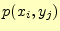 は,メッセージ
は,メッセージ
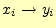 となる確率.
となる確率.
|
|
ここで,
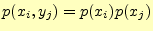 と考える人がいるかもしれない.それは間違いである.次の
ような二元対称通信路(図4)を考えれば,明らかである.
と考える人がいるかもしれない.それは間違いである.次の
ような二元対称通信路(図4)を考えれば,明らかである.
- 誤りが全く生じない場合を考える.送信者が'0'を送れば,受信者は必ず'0'を受
け取る.反対に'1'を送れば,'1'を受け取る.
- 送信者が'0'および'1'を送る確率は,それぞれ0.5である.すなわち,
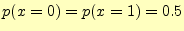 となる.
となる.
- 途中で誤りが全く生じないので,受信者が'0'および'1'を受け取る確率はそれぞれ
0.5である.すなわち,
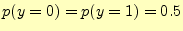 となる.
となる.
- 従って,
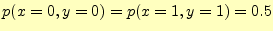 ,
,
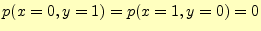 となる.
となる.
この場合,明らかに
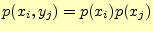 は成立しない.この関係式が成り立つの
は,入出力がお互いに全く無関係の場合のみである.このような通信路は全く役に立たな
い!! 2元対称通信路の場合,誤りの確率が
は成立しない.この関係式が成り立つの
は,入出力がお互いに全く無関係の場合のみである.このような通信路は全く役に立たな
い!! 2元対称通信路の場合,誤りの確率が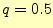 のときである.
のときである.
図:
通信路の途中で誤りが発生しない2元対称通信路の確率.この場合,明らかに
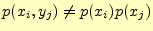 である.
である.
|
|
元に戻って,今後のために一般的な2次元対通信路の確立の関係を示しておく.全て,直
感的に理解できる式である.
これらの式は,式(2)や式(3)に対応したものである.
神様になった気持ちでシステム全体を見渡して,エントロピー(平均情報量)を考える.こ
のシステムを観測することにより得られる情報は,送信者の文字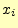 と受信者の文字
と受信者の文字
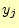 である.送受信が
である.送受信が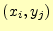 となる確率は
となる確率は
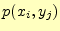 なので,エントロピー
なので,エントロピー
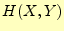 は
は
である.これを,結合エントロピーと呼ぶ.また,システムエントロピーと呼ばれること
もある.
これは,ある一つの通信を行ったとき,送信/受信の両方の文字を知ることにより,得
ることができる平均情報量である.あるいは,このシステムの通信前の情報の平均的な情
報の曖昧(不確かさ)の度合いを表していると言っても良い.
1回通信を行い,送信/受信の文字を知ることにより,情報が確定する;曖昧さがなくなる.
確率の低い情報ほど大きな情報を得ることができる.確率と情報量の関係は,
情報量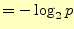 |
(9) |
であった.ここで,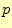 はその情報が生じる確率である.底の2は大きな意味は無く,他で
も良いがバイナリーデータを扱うことが多いので,その方が都合が良い.これから,結合
エントロピーは,得られる情報量の期待値であることが分かる.これは,以前学習したと
おり.
次に受信者側を考える.この場合でも,受け取る文字に関するエントロピー(平均情報量
)は,
はその情報が生じる確率である.底の2は大きな意味は無く,他で
も良いがバイナリーデータを扱うことが多いので,その方が都合が良い.これから,結合
エントロピーは,得られる情報量の期待値であることが分かる.これは,以前学習したと
おり.
次に受信者側を考える.この場合でも,受け取る文字に関するエントロピー(平均情報量
)は,
となる.受信者が文字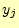 を受け取ると,平均的に
を受け取ると,平均的に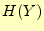 の情報を得る.
の情報を得る.
つぎに,文字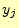 を受け取ったときに,送信者が送った文字を推定することを考える.
文字
を受け取ったときに,送信者が送った文字を推定することを考える.
文字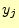 を受け取ったときに,送信文字
を受け取ったときに,送信文字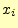 に関してどれだけの情報を得ることができ
るか?--と言う問題である.
に関してどれだけの情報を得ることができ
るか?--と言う問題である.
いま,受信者が文字'0'を受け取ったとする.このとき,
| 送信文字が'0'である確率 |
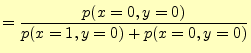 |
|
| |
式(7)を使うと |
|
| |
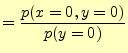 |
(11) |
となる.これを
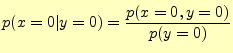 |
(12) |
と表し,条件付き確率と呼ぶ.文字'0'を受け取ったとき,送信文字が'0'である確率であ
る.同様に,文字'0'を受け取ったときに,送信文字が'1'である確率は,
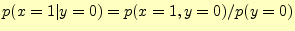 となる.したがって,文字'0'を受け取った場合,入力
文字のあいまいさ(エントロピーあるいは平均情報量)は
となる.したがって,文字'0'を受け取った場合,入力
文字のあいまいさ(エントロピーあるいは平均情報量)は
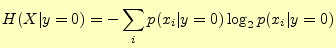 |
(13) |
となる.
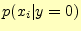 は受け取った文字が'0'のとき,送信した文字が
は受け取った文字が'0'のとき,送信した文字が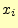 である確率で
ある.
である確率で
ある.
以上のことより,受け取った文字が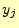 の場合の,送信文字に関するエントロピー
の場合の,送信文字に関するエントロピー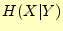 は
は
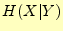 |
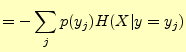 |
(14) |
となる.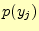 は受け取る文字が
は受け取る文字が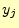 となる確率である.
となる確率である.
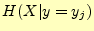 はそのときの
エントロピーである.したがって,
はそのときの
エントロピーである.したがって,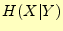 は文字
は文字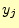 を受け取った後の送信文字に関
する平均的なあいまいさ(条件付きエントロピー)となっている.
を受け取った後の送信文字に関
する平均的なあいまいさ(条件付きエントロピー)となっている.
この式をもう少し変形すると,次のようになる.
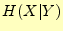 |
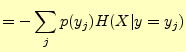 |
|
| |
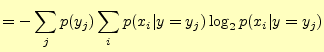 |
|
| |
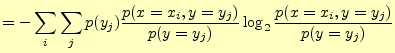 |
|
| |
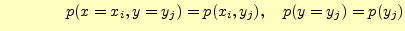 となるので となるので |
|
| |
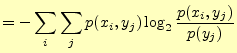 |
|
| |
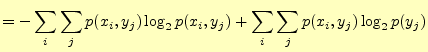 |
|
| |
右辺第一項は,式(8)より |
|
| |
![$\displaystyle =H(X,\,Y) +\sum_j\left[\sum_i p(x_i,y_j)\right]\log_2 p(y_j)$](img137.png) |
|
| |
右辺第二項は,式(3)より |
|
| |
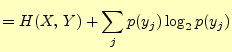 |
|
| |
右辺第二項は,式(10)より |
|
| |
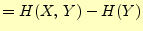 |
(15) |
これは,出力文字を知った後での,入力文字のあいまいさを表している.
これと全く同じ議論が,逆の場合でも成り立つ4.文字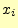 を送ったとき,受
信者が受け取る文字
を送ったとき,受
信者が受け取る文字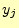 に関するあいまいさでる.式で表すと
に関するあいまいさでる.式で表すと
となる.ここで,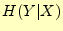 は文字を送信した後に受信者が受け取る文字のあいまいさ(条
件付きエントロピー)である.
は文字を送信した後に受信者が受け取る文字のあいまいさ(条
件付きエントロピー)である.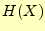 は元々の送信する側の文字のあいまいさである.
は元々の送信する側の文字のあいまいさである.
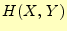 の
の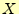 と
と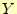 が入れ替わらない理由? これはシステムのエントロピーであり,送
信者側や受信者側とは関係ない,全体に関することである.神様が見ているようなもので,
逆の議論でも関係ない.
文字
が入れ替わらない理由? これはシステムのエントロピーであり,送
信者側や受信者側とは関係ない,全体に関することである.神様が見ているようなもので,
逆の議論でも関係ない.
文字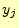 受け取ったとき,送信文字
受け取ったとき,送信文字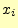 について分かったことを考える.文字を受け取る前の受信者が送信文字
について分かったことを考える.文字を受け取る前の受信者が送信文字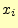 に関して持っているあいまいさ(エントロピー)は,
に関して持っているあいまいさ(エントロピー)は,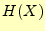 であった.ここで
であった.ここで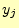 受け取る(観測)とあいまいさは,
受け取る(観測)とあいまいさは,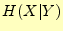 となった.文字
となった.文字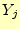 を
受け取ることにより,あいまいさが
を
受け取ることにより,あいまいさが
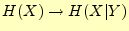 と変化した.この変化した量が受け
取った情報量
と変化した.この変化した量が受け
取った情報量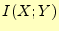 である.したがって,
である.したがって,
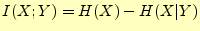 |
(17) |
である.この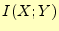 を相互情報量と呼ぶ.式(16)と式
(15)から,
を相互情報量と呼ぶ.式(16)と式
(15)から,
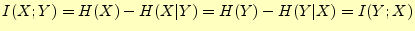 |
(18) |
と書き直すことができる.この式の言っていることは少し不思議な感じがする.つぎの2
つが全く同一となる.
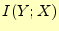 は,文字
は,文字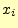 を送った後,受信者が受け取るであろう文字
を送った後,受信者が受け取るであろう文字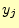 のあい
まいさの減少を表す.
のあい
まいさの減少を表す.
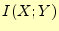 は,文字
は,文字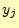 を受け取ると,送信者が送ったであろう文字
を受け取ると,送信者が送ったであろう文字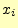 のあい
まいさの減少を表す.
のあい
まいさの減少を表す.
それでは,具体的に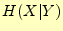 と
と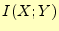 をプロットしてみよう.もっ
とも単純な2次元対称線路を考える.図5に示すように,送
信者が'0'を送る確率
をプロットしてみよう.もっ
とも単純な2次元対称線路を考える.図5に示すように,送
信者が'0'を送る確率
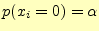 とし,誤りの確率を
とし,誤りの確率を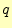 とする.
とする.
図 5:
一般的な2元対称通信路.送信者が'0'を送る確率を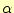 ,通信路の途中
で誤りが生じる確率を
,通信路の途中
で誤りが生じる確率を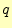 としている.
としている.
|
|
式(15)を使うと,
が得られる.さらに,式(10)を使うと
が得られる.以上より,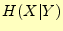 と
と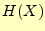 の計算でき,図6
のグラフ(教科書 [1]のp.68の図3.23と同じ)が得られる.
の計算でき,図6
のグラフ(教科書 [1]のp.68の図3.23と同じ)が得られる.
図 6:
2元
対称線路の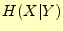 と
と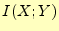 のグラフ.上向きの凸が
のグラフ.上向きの凸が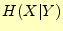 で,凹が
で,凹が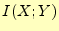 であ
る.横軸は通信路のエラーの確率
であ
る.横軸は通信路のエラーの確率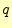 である.
である.
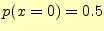 の場合である.
の場合である.
|
|
図6のグラフから,次のことが分かる.
- 条件付きエントロピー
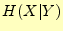 は,文字
は,文字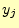 を受け取ったときに送信文字
を受け取ったときに送信文字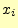 のあいまいさを表している.受信者が送信文字を何かの方法で知ったとき;送信文
字が確定したときに得られる平均情報量(エントロピー)と言ってもよい.グラフ
より以下のことが分かる.
のあいまいさを表している.受信者が送信文字を何かの方法で知ったとき;送信文
字が確定したときに得られる平均情報量(エントロピー)と言ってもよい.グラフ
より以下のことが分かる.
- 通信路でのエラーの確率
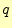 が0または1の時は,条件付きエントロピーは
ゼロである.この場合,即座に送信文字は確定できる.したがって,あいまい
さは全くない.
が0または1の時は,条件付きエントロピーは
ゼロである.この場合,即座に送信文字は確定できる.したがって,あいまい
さは全くない.
- 通信路でのエラーの確率
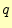 が0.5のとき,条件付きエントロピーは最大に
なる.この場合,文字を受け取っても,全く送信文字の推定ができないか
らである.
が0.5のとき,条件付きエントロピーは最大に
なる.この場合,文字を受け取っても,全く送信文字の推定ができないか
らである.
- 相互情報量
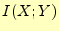 は,文字
は,文字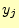 を受け取ったときに,送信文字
を受け取ったときに,送信文字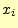 に関して
得る情報量である.グラフより以下のことが分かる.
に関して
得る情報量である.グラフより以下のことが分かる.
- 通信路でのエラーの確率
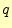 が0または1の時は,相互情報量エントは
最大になる.この場合,即座に送信文字は確定できる.したがって,送信
文字に関して多くの情報を得たことになる.
が0または1の時は,相互情報量エントは
最大になる.この場合,即座に送信文字は確定できる.したがって,送信
文字に関して多くの情報を得たことになる.
- 通信路でのエラーの確率
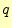 が0.5のとき,相互情報量はゼロに
なる.この場合,文字を受け取っても,全く送信文字に関する情報を得る
ことができないからである.
が0.5のとき,相互情報量はゼロに
なる.この場合,文字を受け取っても,全く送信文字に関する情報を得る
ことができないからである.
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年12月7日
![]() を送る.もし,アルファベット26文字のいずれかを送るなら
ば,
を送る.もし,アルファベット26文字のいずれかを送るなら
ば,
![]() と考える.また,0か1のバイナリーデータを送るならば,
と考える.また,0か1のバイナリーデータを送るならば,
![]() である.ここで,送信者が文字
である.ここで,送信者が文字![]() を送る確率を
を送る確率を![]() とする.すると,
とする.すると,
![]() とする.ここでは,受
け取る文字の確率を
とする.ここでは,受
け取る文字の確率を![]() とする.もちろん,いずれかの文字を受け取るので,その和
は1になる.
とする.もちろん,いずれかの文字を受け取るので,その和
は1になる.
![]() )で,エラーが起きる場合か? この場合,送られるメッセージと受け取るメッ
セージは,
)で,エラーが起きる場合か? この場合,送られるメッセージと受け取るメッ
セージは,
![]() のようになる.受信者は,受け取ったメッセージから送っ
たメッセージが分かる.'0'と'1'を反転させれば良い.エラーが0[%]の時と同じだけ情
報を受け取ることができる.もっとも「質の悪い」エラーは50[%]の確率(
のようになる.受信者は,受け取ったメッセージから送っ
たメッセージが分かる.'0'と'1'を反転させれば良い.エラーが0[%]の時と同じだけ情
報を受け取ることができる.もっとも「質の悪い」エラーは50[%]の確率(![]() )でエラーが発生
する場合である.この場合,受け取るメッセージはランダムに'0'と'1'が並んだ数列に
なり,送信者の送った情報を全く受け取ることができない3.
)でエラーが発生
する場合である.この場合,受け取るメッセージはランダムに'0'と'1'が並んだ数列に
なり,送信者の送った情報を全く受け取ることができない3.
送信者が文字
を送信する確率.
受信者が文字
を受け取る確率.
送信者が
を送り,受信者が
を受け取る確率.
![]() と考える人がいるかもしれない.それは間違いである.次の
ような二元対称通信路(図4)を考えれば,明らかである.
と考える人がいるかもしれない.それは間違いである.次の
ような二元対称通信路(図4)を考えれば,明らかである.
![]() を受け取ったときに,送信者が送った文字を推定することを考える.
文字
を受け取ったときに,送信者が送った文字を推定することを考える.
文字![]() を受け取ったときに,送信文字
を受け取ったときに,送信文字![]() に関してどれだけの情報を得ることができ
るか?--と言う問題である.
に関してどれだけの情報を得ることができ
るか?--と言う問題である.
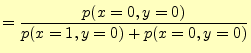
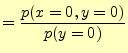
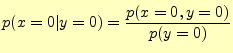
![]() の場合の,送信文字に関するエントロピー
の場合の,送信文字に関するエントロピー![]() は
は
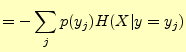
![]() を送ったとき,受
信者が受け取る文字
を送ったとき,受
信者が受け取る文字![]() に関するあいまいさでる.式で表すと
に関するあいまいさでる.式で表すと