アナログデータをデジタルデータに変換する場合,ある等間隔2の時刻で信号を観 測する.先ほどのマイクロフォンから出てくる電圧であれば,図2 のように観測する.図中の●が観測データである.このようにデータを取り出す操作を標 本化(sampling)と呼ぶ.
時刻を等間隔で区切って観測するように,電圧も等間隔に区切る.電圧の区切る話は,次 の「量子化」で述べる.
標本化により取り出させたデータは,数値化されて保存できる.図1のよ うなアナログ量が連なった数値(数列)として,表されたことになる.このように数値の列 に情報を表現すると,コンピューターでは容易に取り扱うことができる.このようなデー タをデジタルデータと呼ぶ.
もちろん,この数列から,元のアナログ信号を再構成できなくては,意味がない.再構成 した様子を図3に示す.この図から,再構成された信号は元のデータと似て いるが,多少,波形が異なることが分かる.すなわちデータが劣化したのである.データ をデジタル化する場合,このデータの劣化は避けることができない.
![\includegraphics[keepaspectratio, scale=0.75]{figure/sampling_AD.eps}](img2.png)
|
音声信号を10ビットで量子化することを考える.音声信号は,-5[V]〜5[V]の範囲の電圧
信号とする.10ビットなので,
![]() 段階に分解できる.従って,分解能は,
段階に分解できる.従って,分解能は,
| (1) |
サンプリング間隔が信号の周期よりも長くなると,元の信号の再生ができない.もちろん, これは直感的に理解できる.それでは,信号の周期とサンプリング間隔ではどのような関 係があるのだろうか? これはシャノン(Claude Elwood Shannon,1916-2001)によって,示 された.
サンプリング周波数要するに,信号の周波数がサンプリング周波数の半分以上になるとダメと言うことである. 従って,サンプリング周波数は元の信の周波数の2倍以上にしなくてはならない--とい うことである.サンプリング周波数の半分の周波数をナイキスト周波数という.の半分の周波数以上の周波数はきちんと再生できない.
サンプリング周波数を![]() としたとき,入力信号の周波数(
としたとき,入力信号の周波数(![]() )がナイキスト周波数より
大きいと,その信号周波数が
)がナイキスト周波数より
大きいと,その信号周波数が
![]() として標本化される.このような現象を,エイリアシング
(aliasing)3と呼び,その
様子を図4に示す.この例ではサンプリング周波数が1[KHz]なのでナイキスト周波数は
0.5[kHz]になる.信号の周波数が0.6[kHz]とナイキスト周波数よりも高いので,サンプリ
ング周波数と信号の周波数の差,0.4[kHz]が標本化される.実際の信号と異なるので,非
常にまずいことになる.
として標本化される.このような現象を,エイリアシング
(aliasing)3と呼び,その
様子を図4に示す.この例ではサンプリング周波数が1[KHz]なのでナイキスト周波数は
0.5[kHz]になる.信号の周波数が0.6[kHz]とナイキスト周波数よりも高いので,サンプリ
ング周波数と信号の周波数の差,0.4[kHz]が標本化される.実際の信号と異なるので,非
常にまずいことになる.
CDのサンプリング周波数![]() =44.1[KHz]の場合,ナイキスト周波数は
22.05[kHz]である.音声信号にこのナイキスト周波数以上の信号が混じると,へんな音が
再生されることになる.そのため,信号をAD変換するときには,ローパスフィルターをつ
けて,ナイキスト周波数以上の信号が混じらないようにしている.
=44.1[KHz]の場合,ナイキスト周波数は
22.05[kHz]である.音声信号にこのナイキスト周波数以上の信号が混じると,へんな音が
再生されることになる.そのため,信号をAD変換するときには,ローパスフィルターをつ
けて,ナイキスト周波数以上の信号が混じらないようにしている.
エイリアシングには,いろいろな場面で遭遇する.蛍光灯の下で扇風機を動かし始めると きと止めるときにエイリアシングが起きる.羽がゆっくり回って見えたり,止まったり, 逆回転が見えたりする.また,テレビの中で車のタイヤの回転が同じように見えることが ある.これはすべてエイリアシングが起きている.
![\includegraphics[keepaspectratio, scale=1.0]{figure/aliasing0.eps}](img11.png)
|
なぜこのようなことが生じるか? 考えてみよう.いろいろな説明方法を考えたが,どれも 結構難しい.4年生のときに学習した複素フーリエ級数4を使うとどうだろうか.
サンプリングは,図5の点線の矩形波を信号に乗算していると
考える.この矩形波の幅がゼロ近づく極限5がサンプリング
となる.いくら幅が狭くても,この矩形波![]() は,繰り返し波形なのでフーリエ級数
6で
表すことができるであろう.
は,繰り返し波形なのでフーリエ級数
6で
表すことができるであろう.
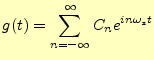 |
(2) |
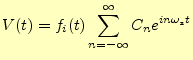 |
(3) |
| (5) |
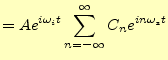 |
||
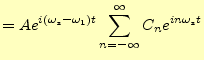 |
||
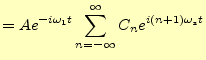 |
||
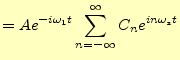 |
(6) |
以上の結果から,サンプリング周波数が1[kHz]の場合,その半分の周波数(0.5[kHz])まで 再生がきちんと再生できることになる.むろん,再生した信号には0.5[kHz]以上を含んで はならない.
諸君が昨年の応用解析で学習したフーリエ変換は数学だったので,関数![]() は連続的な
値であった.しかし,実際の測定量,例えば電圧など連続的に測定してそのデータが蓄え
られるわけではない.連続ではなく離散的なデータとなる.これをフーリエ変換する方法
を示す.
は連続的な
値であった.しかし,実際の測定量,例えば電圧など連続的に測定してそのデータが蓄え
られるわけではない.連続ではなく離散的なデータとなる.これをフーリエ変換する方法
を示す.
ここでも話を簡単にするために,周期を![]() とする.その,周期の中でN個の等間隔で
データが得られたとしよう.いわゆる,サンプリングである.データが等間隔に並ぶとい
うことはFFTで重要となる.ここではFFTまで,話をしない.
とする.その,周期の中でN個の等間隔で
データが得られたとしよう.いわゆる,サンプリングである.データが等間隔に並ぶとい
うことはFFTで重要となる.ここではFFTまで,話をしない.
サンプリングで得られたデータを
| (7) |
| (8) |
準備ができたので,実際のフーリエ級数の式
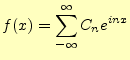 |
(9) |
| (10) |
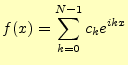 |
(11) |
ここで,サンプリングで得られた![]() 個のデータから,
個のデータから,![]() 個の周波数に分解できることが
理解できた.得られた
個の周波数に分解できることが
理解できた.得られた![]() 個の周波数の振幅は大きいものもあれば,小さいものもある.
小さいものは,信号の再生に寄与が少なく,それを加算しなくても,大体もとの信号と同
じ形になる.従って,寄与の少ない信号を無視することにより,サンプリングのデータ数よ
りも小さいデータ数で再生ができる.これは,データの圧縮に他ならない.
個の周波数の振幅は大きいものもあれば,小さいものもある.
小さいものは,信号の再生に寄与が少なく,それを加算しなくても,大体もとの信号と同
じ形になる.従って,寄与の少ない信号を無視することにより,サンプリングのデータ数よ
りも小さいデータ数で再生ができる.これは,データの圧縮に他ならない.