Subsections
最小二乗法を感覚的に理解するために,最初に一次関数の最小二乗法を示す.その後,一
般的な線形最小二乗法について説明する.非線形最小二乗法は難しいので,範囲外とする.
最小二乗法というのは,データをある関数で最良近似する方法である.例えば,
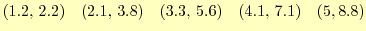 |
(20) |
の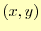 の実験データがあるとする.これを直線で近似
の実験データがあるとする.これを直線で近似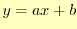 したい.どうすればよ
いか?--という問題である.誤差の二乗が最小になる直線が最良近似とすることができる.
これを最小二乗法(least squares method)と言う.式で表すと,誤差の二乗の和
したい.どうすればよ
いか?--という問題である.誤差の二乗が最小になる直線が最良近似とすることができる.
これを最小二乗法(least squares method)と言う.式で表すと,誤差の二乗の和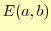 は,
は,
となる.
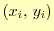 は,
は,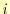 番目のデータで,
番目のデータで,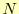 はデータの個数である.この誤差が
最小になる
はデータの個数である.この誤差が
最小になる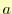 と
と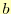 を捜す.式(21)は
を捜す.式(21)は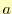 にも
にも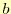 にも2次式でその係
数は正の値なので最小値がある.誤差
にも2次式でその係
数は正の値なので最小値がある.誤差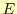 の最小値は,それぞれ偏微分した値がゼロとな
るときに得ることができる.
の最小値は,それぞれ偏微分した値がゼロとな
るときに得ることができる.
| |
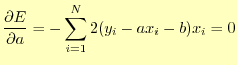 |
|
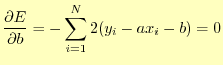 |
|
(22) |
これは,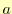 と
と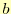 の連立方程式である.すなわち,
の連立方程式である.すなわち,
である.これを解くと
| |
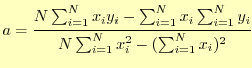 |
|
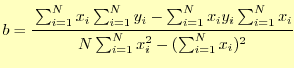 |
|
(24) |
となる.
最初に示したのデータについて計算してみると,
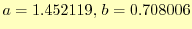 となる.ゆ
えに,最小二乗法による1次関数は
となる.ゆ
えに,最小二乗法による1次関数は
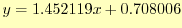 |
(25) |
となる.データをこの間数をプロットすると,図6のようになる.
グラフ作成ソフトウェアーは,最小二乗法によるデータのフィッティングをサポートして
いるものが多い.Excelでも可能なはずである.また,私のWEBページでは
web_gnuplot
と称して,最小二乗法がweb上で使えるようになっている.実験データの整理に使うと良
い.というか,実験データの整理に最小二乗法を使わないことはあり得ない.
ここでは,偏微分により最小二乗法の式を導いたが,線形代数の部分空間への射影を考え
る方が簡単である.これについては,参考文献 [2]に詳しく書い
てある.これは良い教科書なので,一読を勧める.
一次関数の例を拡張して,線形最小二乗法の説明を行う.ただ,ここの線形最小二乗法の
説明は,結構いい加減なところもある.また,線形最小二乗法に適した連立方程式の解き
方も述べていない.最小二乗法について詳細に知りたければ,文献 [3]が大いに
参考になる.本格的な最小二乗法のプログラムを作成するときには,この文献を見ること
を勧める.
データをフィットする線形最小二乗法の関数は,
である.ここで,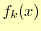 は基底関数(base function)と呼ばれるもので,
は基底関数(base function)と呼ばれるもので,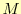 はその個数
である.基底関数は,どのような関数でも良い.例えば,
はその個数
である.基底関数は,どのような関数でも良い.例えば,
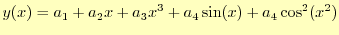 |
(27) |
とすることができる.
ここでは,得られたデータ点
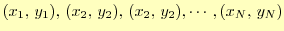 に最も近い係数
に最も近い係数
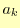 を求めることが問題となる.近いというのは,一次関数の例と同じように,誤差の
二乗和が最小になることを言う.式(26)の場合,誤差の二乗は,
を求めることが問題となる.近いというのは,一次関数の例と同じように,誤差の
二乗和が最小になることを言う.式(26)の場合,誤差の二乗は,
となる.
誤差の二乗和
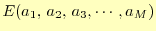 が最小になるように決めれられた係数
が最小になるように決めれられた係数
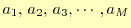 が最良近似となる.これは,それぞれの係数で偏微分した
値がゼロになるようにすれば良い.一次関数の時と全く同じだ! 式で表すと次のようにな
る.
が最良近似となる.これは,それぞれの係数で偏微分した
値がゼロになるようにすれば良い.一次関数の時と全く同じだ! 式で表すと次のようにな
る.
これをよく見ると,次のような連立方程式に書き直すことができる.
この連立方程式を解いて,
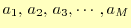 を求めれば,データをフィッ
トする関数の式(26)の最適係数が求まったことになる.
を求めれば,データをフィッ
トする関数の式(26)の最適係数が求まったことになる.
連立方程式(30)の解法については,文献 [3]が詳しい.と
りあえずガウス・ジョルダン法で解いてみて,ダメ(特異に近い)ならば,この文献を参考
にしてプログラムを作成せよ.特異値分解(singular value decomposition, SVD)が良い
ようである.
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
2008-11-23
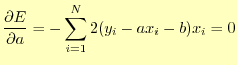
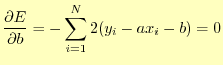
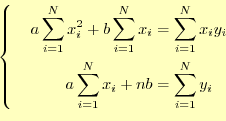
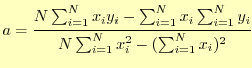
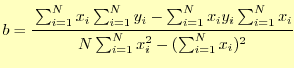
![]() となる.ゆ
えに,最小二乗法による1次関数は
となる.ゆ
えに,最小二乗法による1次関数は
![]() に最も近い係数
に最も近い係数
![]() を求めることが問題となる.近いというのは,一次関数の例と同じように,誤差の
二乗和が最小になることを言う.式(26)の場合,誤差の二乗は,
を求めることが問題となる.近いというのは,一次関数の例と同じように,誤差の
二乗和が最小になることを言う.式(26)の場合,誤差の二乗は,
![]() が最小になるように決めれられた係数
が最小になるように決めれられた係数
![]() が最良近似となる.これは,それぞれの係数で偏微分した
値がゼロになるようにすれば良い.一次関数の時と全く同じだ! 式で表すと次のようにな
る.
が最良近似となる.これは,それぞれの係数で偏微分した
値がゼロになるようにすれば良い.一次関数の時と全く同じだ! 式で表すと次のようにな
る.