ここの説明は,文献 [1]を参考にした.これは線形代数を実際に
どのように応用するか?--を詳細に述べた教科書で工学系の学生は一度は読んでもらいたい.
初めて私が線形代数の講義を受けたとき,あまりにも抽象的で,さっぱりわからなかった.
その後,この教科書を読むことにより,なるほど線形代数は便利なものであるとやっとわ
かったのである.
さて,いままで学習した直接法はしつこく計算すれば,必ず解が求まる.しかし,大きな
連立方程式を計算するには不向きである.なぜならば,ガウス・ジョルダン法の計算回数
は,方程式の次元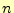 の三乗に比例するため,大きな行列ではとたんに計算時間が必要に
なるからである.
の三乗に比例するため,大きな行列ではとたんに計算時間が必要に
なるからである.
実用的なプログラムでは,非常に大きな連立方程式を計算しなくてはならない.たとえば,
私の研究室での計算でも10万元くらいは計算している.これをガウス・ジョルダン法で計
算すると膨大な時間が必要となり,現実的ではない.そこで,これよりは格段に計算の速
い反復法を用いている.ここでは,その反復法を簡単に説明する.
当然ここでも,連立方程式
を満たす
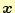 を数値計算で求める.反復法の理論を考えるために,この連立方程式の
真の解
を数値計算で求める.反復法の理論を考えるために,この連立方程式の
真の解
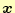 とする.
とする.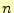 回目の反復計算によりで求められたものを
回目の反復計算によりで求められたものを
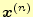 とする.
そして,反復の計算回数を増やして,
とする.
そして,反復の計算回数を増やして,
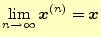 |
(12) |
になったとする.反復の計算方法を上手に選ぶと,真の解に収束させることができる.こ
のように反復計算を行い真の解に収束させる方法を反復法と言う.
どのようにして反復計算をするのか? 例えば,行列
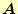 を
を
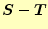 と分解するだけで,反復計算の式を作成することができる.
と分解するだけで,反復計算の式を作成することができる.
ここで,
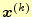 が
が
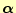 に収束するとする.すると,式
(13)と式(11)を比べれば,
に収束するとする.すると,式
(13)と式(11)を比べれば,
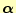 と
と
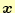 は等しいことがわかる.すなわち,式(13)で元の方程式
(11)を表した場合,
は等しいことがわかる.すなわち,式(13)で元の方程式
(11)を表した場合,
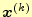 が収束すれば,必ず真の解
が収束すれば,必ず真の解
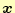 に収束するのである.別の解に収束することはなく,真の解に収束するか,発散
するかのいずれかである.振動することはないのか? それはよい質問である.興味があ
る人が調べてみてほしい.
に収束するのである.別の解に収束することはなく,真の解に収束するか,発散
するかのいずれかである.振動することはないのか? それはよい質問である.興味があ
る人が調べてみてほしい.
言うまでもないと思うが,式(13)をつかって,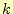 番めの近似解
番めの近似解
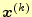 から
から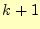 番めの近似解
番めの近似解
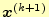 は,
は,
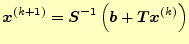 |
(14) |
の計算により求める.この式の中には係数行列
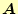 と非同次項の情報は入っており,
情報の過不足はない--ことに注意が必要である.ある意味ではこれは連立方程式の解の
公式と考えることもできる.もちろん,この計算のためには初期値
と非同次項の情報は入っており,
情報の過不足はない--ことに注意が必要である.ある意味ではこれは連立方程式の解の
公式と考えることもできる.もちろん,この計算のためには初期値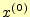 は必要で,
それはプログラマーあるいはユーザー適当に決めなくてはならない.
先の説明で,式(13)を使った反復法の場合,
は必要で,
それはプログラマーあるいはユーザー適当に決めなくてはならない.
先の説明で,式(13)を使った反復法の場合,
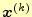 の収束が重要
であることがわかった.ここでは,これが収束する条件を示す.
の収束が重要
であることがわかった.ここでは,これが収束する条件を示す.
真の解の場合,式(13)は
となる.この式(15)から式(13)を引くと,
となる.
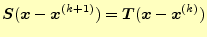 |
(16) |
となる.ここで,
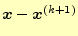 や
や
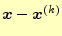 は,真の解からの差,すな
わち,誤差を示している.
は,真の解からの差,すな
わち,誤差を示している.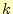 回目の計算の誤差を
回目の計算の誤差を
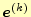 とすると,
とすると,
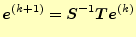 |
(17) |
と表すことができる.この誤差ベクトル
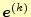 がゼロに収束すれば,ハッピーなのだ.
がゼロに収束すれば,ハッピーなのだ.
ハッピーになるための条件を探すために,計算の最初の誤差を
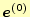 とする.すると,
とする.すると,
となる.この式の右辺には,やっかいそうな行列の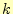 乗の計算がある.しかし,
2.3 節で得た結果を利用するとその計算も簡単である.行列
乗の計算がある.しかし,
2.3 節で得た結果を利用するとその計算も簡単である.行列
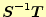 の固有値と固有ベクトルで作る行列を,
の固有値と固有ベクトルで作る行列を,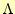 と
と
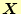 とする
と,式(18)は
とする
と,式(18)は
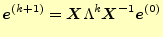 |
(19) |
となる.明らかに,計算回数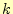 を増やしていくと,誤差のベクトル
を増やしていくと,誤差のベクトル
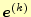 は
は
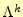 に依存する.これは,
に依存する.これは,
![$\displaystyle \Lambda^k=\left[ \begin{array}{@{\,}ccccc@{\,}} \lambda_1^k & & &...
...ash{\Huge$0$}}\quad} & & \ddots & \\ & & & & \lambda_n^k \\ \end{array} \right]$](img89.png) |
(20) |
となるので,
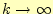 の場合,誤差
の場合,誤差
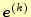 がゼロに収束するために
は,すべての固有値が
がゼロに収束するために
は,すべての固有値が
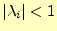 でなくてはならない.そして,収束の速度は,最
大の固有値
でなくてはならない.そして,収束の速度は,最
大の固有値
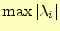 に依存する.この絶対値が最大の固有値をスペクトル半径
と言う.
に依存する.この絶対値が最大の固有値をスペクトル半径
と言う.
ここで言いたいのは,連立方程式を式(13)の反復法で計算する場合,
結果が真の値に収束するためには,行列
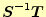 の最大固有値の絶対値が1以
下でなくてはならないと言うことである.
の最大固有値の絶対値が1以
下でなくてはならないと言うことである.
最大固有値が1以下になる行列の条件を探すことは難しい.また,予め行列
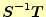 の最大固有値を計算することも考えられるが,それもかなりの計算
量が必要で,反復法を使って計算時間を短縮するメリットが無くなってしまう.このよう
なことから,反復法はとりあえず試してみて,発散するようであれば他の方法に切り替え
るのが良いだろう.後で述べるSOR法の加速緩和係数
の最大固有値を計算することも考えられるが,それもかなりの計算
量が必要で,反復法を使って計算時間を短縮するメリットが無くなってしまう.このよう
なことから,反復法はとりあえず試してみて,発散するようであれば他の方法に切り替え
るのが良いだろう.後で述べるSOR法の加速緩和係数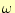 を1以下にするという方法も
ある.
を1以下にするという方法も
ある.
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年11月8日
![]() を
を
![]() と分解するだけで,反復計算の式を作成することができる.
と分解するだけで,反復計算の式を作成することができる.
![]() 番めの近似解
番めの近似解
![]() から
から![]() 番めの近似解
番めの近似解
![]() は,
は,
![]() とする.すると,
とする.すると,
![$\displaystyle \Lambda^k=\left[ \begin{array}{@{\,}ccccc@{\,}} \lambda_1^k & & &...
...ash{\Huge$0$}}\quad} & & \ddots & \\ & & & & \lambda_n^k \\ \end{array} \right]$](img89.png)
![]() の最大固有値の絶対値が1以
下でなくてはならないと言うことである.
の最大固有値の絶対値が1以
下でなくてはならないと言うことである.
![]() の最大固有値を計算することも考えられるが,それもかなりの計算
量が必要で,反復法を使って計算時間を短縮するメリットが無くなってしまう.このよう
なことから,反復法はとりあえず試してみて,発散するようであれば他の方法に切り替え
るのが良いだろう.後で述べるSOR法の加速緩和係数
の最大固有値を計算することも考えられるが,それもかなりの計算
量が必要で,反復法を使って計算時間を短縮するメリットが無くなってしまう.このよう
なことから,反復法はとりあえず試してみて,発散するようであれば他の方法に切り替え
るのが良いだろう.後で述べるSOR法の加速緩和係数![]() を1以下にするという方法も
ある.
を1以下にするという方法も
ある.