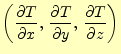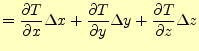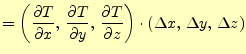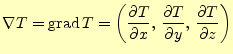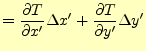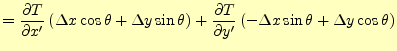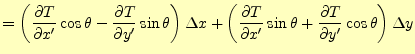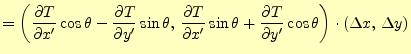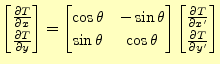3 スカラー場の勾配(
 )
)
3.1 勾配の定義
連続的になめらかに変化するスカラー場では,2次元では等高線,3次元では等高面を描く ことができる.その等高線や等高面は次のような性質がある.- 閉じているか,考えている空間でいっぱいに広がっているのどちらかである.
- 決して交わることは無い.
ここでは,スカラー場の例とて温度分布を考える.頭の中で,温度のイメージ
を描くことは簡単ので,スカラー場の例に使う.しかし,ここでの話は温度の
みならず,スカラー場一般について成り立つ.この温度は,位置の関数なので
![]() と書くことができる.このような関数の場合,いろいろな微分
を考えることができる.たとえば,
と書くことができる.このような関数の場合,いろいろな微分
を考えることができる.たとえば,
| (1) |
である.これは,座標軸の取り方に依存してる.座標軸を変えれば,値が変わってしまう のは明らかである.従って,スカラー量はないし2,ベクトル量でない3のも明らかである.スカラー量でもベクトル量でも無いものは, 座標軸を変えると式が変わってしまい,物理的な考察をするときには役に立たない.
まだ他に,スカラー場の微分はいろいろ考えられる.しかし,実際問題,スカラー場の微分で役に 立つのは,勾配
と呼ばれる量である.私は,これ以外の微分に出会ったことはない.スカラー場の微分で 役に立つものはこれしか無いと考えよい.
この勾配には3つの成分があり,ベクトル場になっている.それぞれは,位置の関数であ
るので場の量であることは確かである.また,![]() はなめらかな関数なので,この3成分
もなめらかに変化するのも確かである.後の問題は,この3成分がベクトル量であること
を示せば良い.それを2つの方法で示す.
はなめらかな関数なので,この3成分
もなめらかに変化するのも確かである.後の問題は,この3成分がベクトル量であること
を示せば良い.それを2つの方法で示す.
式(2)がベクトルであることを示す.非常に近くの2点の温度を考える.
それぞれを
![]() と
と
![]() とす
る.温度差は,
とす
る.温度差は,
![$\displaystyle \simeq \left[T(x,\,y,\,z) + \if 11 \frac{\partial T}{\partial x} ...
...z} \else \frac{\partial^{1} T}{\partial z^{1}}\fi \Delta z \right]-T(x,\,y,\,z)$](img12.png) |
||
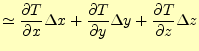 |
(3) |
となる.2点の距離を0の極限まで近づけると,最後の式は等号で結ばれることになる.そ して,変位ベクトル
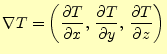 |
(4) |
を導入すると
となる.左辺は温度差なので座標軸を回転させても値は変わらないから,スカラー量であ る.変位
である.
つぎに式(6)がベクトル量になっていることを,座標軸の回転により証
明しよう.3次元は大変なので2次元の場合で説明するが,3次元に拡張しても同じことが
言える.元の座標を
![]() ,それを
,それを ![]() 回転させた座標を
回転させた座標を
![]() とした場合,それらには,
とした場合,それらには,
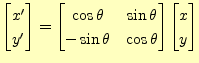 |
あるいは | 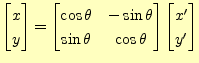 |
(7) |
という関係がある.変位ベクトル
| (8) | ||
| (9) |
となる.先ほどと同じように距離を無限小にとった場合の温度差をプライムが付いた座標 系で考える.温度変化は,
となる.この式の右辺の左側のベクトルと式(5)の2次元 の場合を比較すると,
となる.これを見て分かるように,
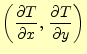 |
(12) |
はという量は,座標軸の回転に対して,座標が受けるのと同じ変換を受ける.従って,ベ クトル量である.これと同じことが,3次元の式(6)についても成り立つ のでベクトル量である.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年5月26日