4 差分法による偏微分方程式の数値計算
4.1 ラプラス方程式
2次元のラプラス方程式を数値計で解くことを考える.まずは,いつものように,解
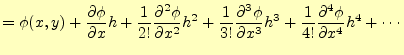 |
(17) | |
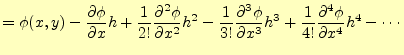 |
(18) |
となる.これらの式の辺々を足し合わせえると,
が得られる.このことから,2階の偏導関数の値は微小変位
が得られる.
これらの式(19)と(20)を元の2次元ラプラス 方程式(16)に代入すれば,
となる.これが,2次元ラプラス方程式の差分の式である.この式を眺めると,座標
実際にこの式を数値計算する場合,計算領域を間隔![]() で格子状3に区切り,その交点での値を求めることになる.
ここでは,xおよびy方向には等間隔
で格子状3に区切り,その交点での値を求めることになる.
ここでは,xおよびy方向には等間隔![]() で区切り計算を進めるが,等間隔である必要はな
い.多少,式(21) は異なるが同じような計算は可能である.これまでの説
明が理解できていれば,xとy方向の間隔が異なっても,式(21)に対応する差
分の式が作れるはずである.
で区切り計算を進めるが,等間隔である必要はな
い.多少,式(21) は異なるが同じような計算は可能である.これまでの説
明が理解できていれば,xとy方向の間隔が異なっても,式(21)に対応する差
分の式が作れるはずである.
実際,数値計算をする場合,![]() や
や
![]() の形は不便なので,形式を改め
る.各格子点でのポテンシャルを
の形は不便なので,形式を改め
る.各格子点でのポテンシャルを
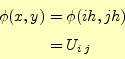 |
(22) |
とする.このようにすると,式(21)は
となり,数値計算し易い形になる.
ラプラス方程式は式(23)の連立方程式を解くだけである.格子に領域を分 割することにより,難しげな偏微分方程式が連立方程式に還元されたわけである.
連立方程式を解くわけであるが,このままでは,式の数と未知数の数が異なる.格子点で のポテンシャルの値を求めるためには,境界条件を設定する必要がある.それにより,式 の数と未知数の数が同一になり,格子点でのポテンシャルを求めることができる.
4.2 波動方程式
弦の長さが1,そこを伝わる波の速度を1として,弦の横波の様子を数値計算で解くことを 考える.1次元波動方程式をコンピューターを用いて近似計算するのである.計算に移る 前に,解くべき方程式と条件をきちんと書いておく.解くべき方程式と条件は,となる.この最初の式は波動方程式,2番目を初期条件,3番目を境界条件と言う.
波動方程式を解くためには,初期条件と境界条件が必要である.ある時刻の位置と速度が 決まれば,それ以降を力学的状態は決まってしまう--ということに対応している.振動 の場合は,これに加えて更に,振動の境界条件を決める必要がある.これらが決まって初 めて,振動の状態--ある時刻の変位と速度--が決まるわけである.図4に 初期条件と境界条件の様子を示す.
まずは,波動方程式を差分方程式に書き直すことからはじめる.これも,いつものように,
解![]() をテイラー展開する.x方向の微小変位を
をテイラー展開する.x方向の微小変位を![]() ,時間軸方向の微小変位
を
,時間軸方向の微小変位
を![]() とする.すると,
とする.すると,
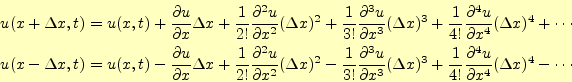 |
(25) |
となる.これらの式の辺々を足し合わせえると,
が得られる.このことから,2階の偏導関数の値は微小変位
が得られる.
これらの式(26)と(27)を元の波動 方程式(24)に代入すれば,
となる.これが,1次元波動方程式の差分の式である.この式を計算し易いよ うに,もう少し変形すると,
とすることができる.この式の右辺は,時刻
実際に式(29)を数値計算する場合,x方向には![]() ,時間
軸方向には
,時間
軸方向には![]() 毎に分割する.ラプラス方程式を格子点で分割したのと
同じである.格子点に分割し数値計算する場合,
毎に分割する.ラプラス方程式を格子点で分割したのと
同じである.格子点に分割し数値計算する場合,![]() や
や
![]() と表現する
よりは,
と表現する
よりは,![]() と表現したほうが便利である.そこで,
と表現したほうが便利である.そこで,
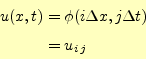 |
(30) |
と表現を改める.このようにすると,式(29)は
となり,数値計算し易い形になる.ただし,
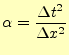 |
(32) |
である.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年2月5日
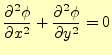
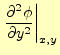
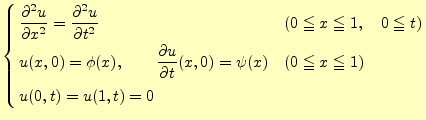
![\includegraphics[keepaspectratio, scale=0.85]{figure/wave_init.eps}](img136.png)
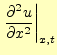
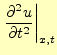
![$\displaystyle u(x,t+\Delta t)= 2u(x,t)-u(x,t-\Delta t)+ \frac{\Delta t^2}{\Delta x^2}\left[ u(x+\Delta x,t)-2u(x,t)+u(x-\Delta x,y) \right]$](img148.png)