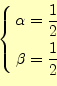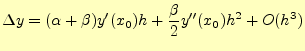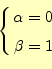数値計算により,近似解を求める微分方程式は,
である.これは問題として与えられ,この式に従う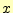 と
と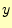 の関係を計算する.これを計
算するためには,テイラー展開が重要な役割を果たす.テイラー展開を計算してから,オ
イラー法,2次のルンゲ・クッタ法を説明する.
数値計算は言うに及ばず科学技術全般の考察にテイラー展開(Taylor expansion)は,重要
な役割を果たす.電気の諸問題を考察する場合,いたるところにテイラー展開は顔を出す
ので,十分理解しなくてはならない.まずは,
の関係を計算する.これを計
算するためには,テイラー展開が重要な役割を果たす.テイラー展開を計算してから,オ
イラー法,2次のルンゲ・クッタ法を説明する.
数値計算は言うに及ばず科学技術全般の考察にテイラー展開(Taylor expansion)は,重要
な役割を果たす.電気の諸問題を考察する場合,いたるところにテイラー展開は顔を出す
ので,十分理解しなくてはならない.まずは,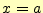 の回りのテイラー展開は,
の回りのテイラー展開は,
と書ける.0の階乗は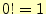 となることに注意.
となることに注意.
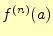 は,関
数
は,関
数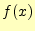 を
を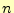 回微分したときの
回微分したときの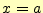 の値である.テイラー展開は,任意の関数
の値である.テイラー展開は,任意の関数
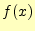 は,無限のべき級数に展開できると言っている.その係数が,
は,無限のべき級数に展開できると言っている.その係数が,
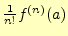 である.次に,
である.次に,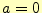 としてみる.この場合,
としてみる.この場合,
となる.これがマクローリン展開(Maclaurin expansion)である.次に
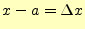 とする.そして,
とする.そして,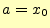 とすると
とすると
となる.これは,しばしばお目にかかるパターン.
通常,我々がテイラー展開を使う場合,この式
(10)〜式(12)
のいずれかである.
常微分方程式の解を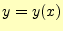 とする.その
とする.その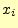 のまわりのテイラー展開は,
のまわりのテイラー展開は,
である.この式の右辺第2項は,式(9)
から計算できる.したがって,テイラー展開は,次のように書き表わせる.
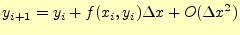 |
(14) |
オイラー法での数値計算では,計算の刻み幅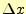 は十分に小さいとして,
は十分に小さいとして,
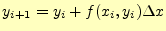 |
(15) |
を計算する.この場合,計算の精度は1次と言う4.
オイラー法では,次の漸化式に従い数値計算を進める.解である
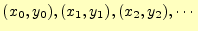 が同じ手続きで計算できる.
実際にプログラムを行うときは,forやwhileを用いて繰り
返し計算を行い,結果の
が同じ手続きで計算できる.
実際にプログラムを行うときは,forやwhileを用いて繰り
返し計算を行い,結果の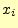 と
と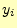 は,配列x[i] や
y[i]に格納するのが常套手段である.
は,配列x[i] や
y[i]に格納するのが常套手段である.
この方法の計算のイメージは,図9の通りである.明らか
に,出発点の導関数のみ利用しているために精度が悪いことが理解できる.式
も対称でないため,逆から計算すると元に戻らない.
図 9:
オイラー法.ある区間での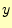 の変化
の変化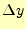 は,計算の始めの
点の傾きに区間の幅
は,計算の始めの
点の傾きに区間の幅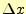 を乗じて,求めている.
を乗じて,求めている.
|
|
次の微分方程式
| |
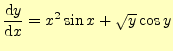 |
|
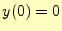 |
|
(17) |
の近似解をオイラー法で計算するプログラムをリスト3に示す.計算結果
は,ファイルに格納している.計算領域は
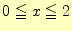 ,計算のステップ幅は
,計算のステップ幅は
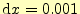 となっている.
となっている.
1 #include <stdio.h>
2 #include <math.h>
3 #define NSTEPS 2000 // 計算ステップ数
4 #define NDIM 30000 // 用意する配列の大きさ
5 #define X_MAX 2.0 // 計算する最大 x
6
7 double f(double x, double y); // プロトタイプ宣言
8
9 //============================================================
10 // main 関数
11 //============================================================
12 int main(void){
13 double x[NDIM], y[NDIM]; // 計算結果を入れる
14 double dx;
15 int i;
16 FILE *out; // 計算結果を保存するファイル
17
18
19 dx = X_MAX/NSTEPS; // 計算のきざみ幅dxの計算
20 x[0] = 0;
21 y[0] = 0;
22
23
24 //------- オイラー法の計算 --------
25
26 for(i=0; i<NSTEPS; i++){
27 x[i+1] = x[0]+(i+1)*dx; //x[i+1]=x[i]+dxよりも精度が良い
28 y[i+1] = y[i]+f(x[i],y[i])*dx;
29 }
30
31
32 //------- 計算結果をファイルに保存 --------
33
34 out = fopen("result.txt","w");
35 for(i=0; i<=NSTEPS; i++){
36 fprintf(out,"%20.15f\t%20.15f\n", x[i],y[i]);
37 }
38
39
40 fclose(out);
41
42 return 0;
43 }
44
45 //============================================================
46 // dy/dx = f(x,y) の f(x,y)を計算する関数
47 //============================================================
48 double f(double x, double y){
49 return x*x*sin(x)+sqrt(y)*cos(y);
50 }
2次のルンゲ・クッタと呼ばれる方法は,いろいろある.ここでは,ホイン法と中点法をしめす.
先に示したように,オイラー法の精度は1次であるが,2次のルンゲ・
クッタ法では2次となる.今まで刻み幅を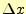 と記述していたが,簡単のため
と記述していたが,簡単のため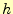 と
表現する.
と
表現する.
2次の精度ということは,テイラー展開より
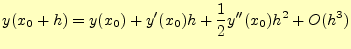 |
(18) |
となっていることを意味する.即ち,計算アルゴリズムが,
となっている.
式(19)から分かるように,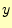 の増分
の増分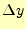 を計算する
ためには,1階微分と2階微分の2項を満たす式が必要である.そうすると少なく
とも,2点の値が必要となる.2点として,計算区間の両端の導関数の値を
使う.この導関数は問題として与えられているので,計算は簡単である.そ
うして,区間の増分を
を計算する
ためには,1階微分と2階微分の2項を満たす式が必要である.そうすると少なく
とも,2点の値が必要となる.2点として,計算区間の両端の導関数の値を
使う.この導関数は問題として与えられているので,計算は簡単である.そ
うして,区間の増分を
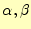 をパラメーターとした和で表すことに
する.即ち,以下の通りである.
をパラメーターとした和で表すことに
する.即ち,以下の通りである.
この
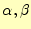 を上手に選ぶことにより,式(19)と同
一にできる.この式を
を上手に選ぶことにより,式(19)と同
一にできる.この式を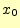 の回りでテイラー展開すると
の回りでテイラー展開すると
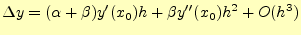 |
(21) |
となる.これを,式(19)と比較すると,
とすれば良いことが分かる.これで,必要な式は求まった.まとめる
と,式(9)を数値計算で近似解を求める
には次式を使うことになる.
この式は,図10のようになる.オイラー法の図
9との比較でも,精度が良いことが分かる.
図 10:
ホイン法(教科書の方法).ある区間での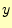 の変化
の変化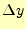 は,
計算の始めと終わりの点付近の平均傾きに区間の幅
は,
計算の始めと終わりの点付近の平均傾きに区間の幅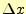 を乗じて,求
めている.
を乗じて,求
めている.
|
|
これも,ホイン法と同じ2次の精度である.ホイン法は区間の両端の点の導関数
を使ったが,中点法は出発点と中点で漸化式を作る.先ほど同様,2点を使うので,2次の精度
にすることができる.ホイン法の式(20)に対応するものは,
である.これを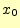 の回りでテイラー展開すると,
の回りでテイラー展開すると,
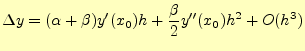 |
(25) |
となる.これを,式(19)と比較すると,
となる必要がある.したがって,中点法の漸化式は,
となる.この公式のイメージを,図11に示しておく.
図 11:
中点法.ある区間での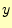 の変化
の変化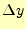 は,中点付近の傾きに
区間の幅
は,中点付近の傾きに
区間の幅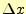 を乗じて,求めている.
を乗じて,求めている.
|
|
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成18年10月2日
![]() は十分に小さいとして,
は十分に小さいとして,
![]() が同じ手続きで計算できる.
実際にプログラムを行うときは,forやwhileを用いて繰り
返し計算を行い,結果の
が同じ手続きで計算できる.
実際にプログラムを行うときは,forやwhileを用いて繰り
返し計算を行い,結果の![]() と
と![]() は,配列x[i] や
y[i]に格納するのが常套手段である.
は,配列x[i] や
y[i]に格納するのが常套手段である.
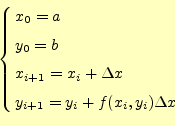
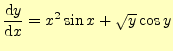
![]() の増分
の増分![]() を計算する
ためには,1階微分と2階微分の2項を満たす式が必要である.そうすると少なく
とも,2点の値が必要となる.2点として,計算区間の両端の導関数の値を
使う.この導関数は問題として与えられているので,計算は簡単である.そ
うして,区間の増分を
を計算する
ためには,1階微分と2階微分の2項を満たす式が必要である.そうすると少なく
とも,2点の値が必要となる.2点として,計算区間の両端の導関数の値を
使う.この導関数は問題として与えられているので,計算は簡単である.そ
うして,区間の増分を
![]() をパラメーターとした和で表すことに
する.即ち,以下の通りである.
をパラメーターとした和で表すことに
する.即ち,以下の通りである.