2 差分法による偏微分方程式の数値計算
2.1 差分方程式
二次元のラプラス方程式を数値計算で近似解を求めることを考える.まずは,いつものよう に,解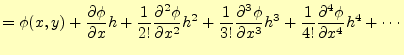 |
(3) | |
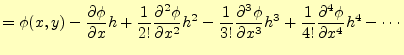 |
(4) |
となる.これらの式の辺々を足し合わせえると,
が得られる.このことから,2階の偏導関数の値は微小変位
が得られる.
これらの式(5)と(6)を元の2次元ラプラス 方程式(2)に代入すれば,
となる.これが,2次元ラプラス方程式の差分の式である.この式を眺めると,座標
実際にこの式を数値計算する場合,例えば図1のポテンシャルを求め
る時には,図5のように格子状2に区切り,その交点での値を求めることになる.ここでは,
![]() および
および![]() 方向には等間隔
方向には等間隔![]() で区切り計算を進めるが,等間隔である必要はない.そ
のようにしても差分の方程式は複雑になるが,同じような計算は可能である.これまでの説明が理解で
きていれば,
で区切り計算を進めるが,等間隔である必要はない.そ
のようにしても差分の方程式は複雑になるが,同じような計算は可能である.これまでの説明が理解で
きていれば,![]() と
と![]() 方向の間隔が異なっても,式(7)に対応する差分の式が作
れるはずである.
方向の間隔が異なっても,式(7)に対応する差分の式が作
れるはずである.
数値計算をする場合,![]() や
や
![]() の形は不便なので,形式を
改める.図4の左下の座標を(0,0)として,格子点で
のポテンシャルを
の形は不便なので,形式を
改める.図4の左下の座標を(0,0)として,格子点で
のポテンシャルを
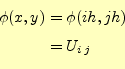 |
とする.このようにすると,式(7)は
となり,数値計算し易い形になる.このようにした場合の各格子点の様子を図 5に示す.
次の節で述べる境界条件を考えないとすると,ラプラス方程式は式(9)の 連立方程式を解くだけである.格子に領域を分割することにより,難しげな偏微分方程式 が連立方程式に還元されたわけである.
2.2 境界条件(外周)
実際に,連立方程式(9)を計算する場合,困った問題が生じる.このまま だと,式の数と未知数の数が合わないのである.たとえば,図6 に示す境界を考える.すると,境界が式9の
そこで,境界上の格子点
![]() 個の値を予め決める.こうすれば,式の数を減らさ
ないで,未知数の数を減らすことができる.要するに偏微分方程式を解くときの境界条件
を決めるのと同じ.驚いたことに,外周部(境界条件)の格子点の数が,ちょうど,不足し
ている方程式の数と同じなのである.自然は,都合良くできているのである.
個の値を予め決める.こうすれば,式の数を減らさ
ないで,未知数の数を減らすことができる.要するに偏微分方程式を解くときの境界条件
を決めるのと同じ.驚いたことに,外周部(境界条件)の格子点の数が,ちょうど,不足し
ている方程式の数と同じなのである.自然は,都合良くできているのである.
懸命な諸君であれば,予め決める値は外周の境界上の格子点でなくても良いと考えるだろ う.しかし,内部の点の値を決めてしまうと,連立方程式が1個減ってしまうので,未知 数と式の数の差は変わらない.これについては,良い説明が思い浮かばなかったので,そ ういうものだと思ってください.
2.3 境界条件(内部の電極)
先ほどの説明通り内部の格子点のポテンシャルを決めてしまうと,その数だけ方程式が減 少する.したがって,必要なだけ内部のポテンシャルを決めても,式と未知数の数は同 じで,連立方程式は解ける.そのような理由で,図5 の電極内部の格子点のポテンシャルホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年1月15日
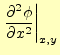
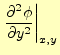
![\includegraphics[keepaspectratio, scale=1.0]{figure/lattice.eps}](img34.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/sabun.eps}](img39.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/eq_boundary.eps}](img44.png)