3 シンプソンの公式
3.1 基本的な考え方
台形公式の考え方は簡単であるが,精度はあまりよくない.そこで,よく似た考え方で精 度が良いシンプソンの公式を説明する.台形公式は,分割点の値を一次関数(直線)で近似 を行い積分を行った.要するに折れ線近似である.ここで,1次関数ではなく,高次の関 数で近似を行えばより精度が上がることは,直感的に分かる.
2次関数で近似を行うことを考える.2次関数で近似するためには,3点必要である.3つの
分点をそれぞれ,
![]() とする.そして,この2次関数を
とする.そして,この2次関数を![]() と
する.
と
する.![]() はラグランジュ補間に他ならないので,
はラグランジュ補間に他ならないので,
となる.図3に示すとおりである.
これを,区間
![]() で積分する.紙面の都合上,式
(11)の右辺を各項毎に積分を行う.まず,右辺第1項で
あるが,それは以下のようになる.
で積分する.紙面の都合上,式
(11)の右辺を各項毎に積分を行う.まず,右辺第1項で
あるが,それは以下のようになる.
同様に,第2,3項を計算すると
となる.以上より,近似した2次関数
となる.
これは,ある区間
![]() の積分で,その巾は
の積分で,その巾は![]() である.区間
である.区間![]() にわ
たっての積分
にわ
たっての積分![]() は,式(15)を足し合わせればよい.ただし,
は,式(15)を足し合わせればよい.ただし,
![]() と足し合わせる.
と足し合わせる.
これが,シンプソンの公式と呼ばれるもので,先ほどの台形公式よりも精度が良い.誤差 は,
注意シンプソンの公式を使う場合,分割数![]() は偶数でなくてはならない.これに
注意して,プログラムを作成しよう.
は偶数でなくてはならない.これに
注意して,プログラムを作成しよう.
3.2 シンプソンの公式の実際の数値積分
実際にシンプソンの公式を使って数値積分を行う場合,台形公式を上手に使う.台形公式からど うやってシンプソンの公式を計算するのか?--という驚きの疑問が湧くだろう.それをこ れから示す.ここでは,基礎となる計算のアルゴリズムとフローチャートを示す.ここの お話は,主に文献 [1]を参考にした2.3.2.1 計算アルゴリズム
区間これから,面白いことに気がつくだろう.どちらも,関数の値を計算するポイントは
図4や式(17)や(18)を見
ると台形公式とシンプソンの公式はよく似ており,なんらかの関係があることは容易に推
測がつく.それらの関係を考えることにする.区間![]() を
を![]() で分割して,数値積
分を行うとする.この時の台形公式の結果を
で分割して,数値積
分を行うとする.この時の台形公式の結果を![]() ,シンプソンの公式の結果を
,シンプソンの公式の結果を![]() とす
る.すると,それらには,
とす
る.すると,それらには,
の関係がある.これは,次のように右辺を計算すれば簡単に証明できる.これを計算する ために,
![$\displaystyle =\frac{4h}{3}\left[ \frac{1}{2}f(a)+f(a+h)+f(a+2h)+f(a+3h)+\cdots+f(b-h)+\frac{1}{2}f(a)f(b) \right]$](img66.png) |
||
![$\displaystyle \qquad-\frac{2h}{3}\left[ \frac{1}{2}f(a)+f(a+2h)+f(a+4h)+f(a+6h)+\cdots+f(b-2h)+\frac{1}{2}f(a)f(b) \right]$](img67.png) |
||
![$\displaystyle =\frac{h}{3}\left[ f(a)+4f(a+h)+2f(a+2h)+4f(a+3h)+\cdots+2f(b-2h)+4f(b-h)+f(b) \right]$](img68.png) |
(19) |
となる.
これまでの結果から,![]() と
と![]() に分割したときの台形公式の積分の値が分
かると,
に分割したときの台形公式の積分の値が分
かると,![]() のときのシンプソンの公式での積分値が計算できると言える.式
(19)のとおりである.しかし,式(18)を
直に計算する方法とどれほどのメリットがあるのだろうか?--という疑問も湧くだろう.
これだけだと,少し計算が早いかもしれないが,それほど大きなメリットはない.ただ,
台形公式と比べると,大変大きなメリットがある.台形公式とほとんど同じ計算で,シン
プソンの公式の精度が得られるのである.ロンバーグ積分まで考えると,さらに大きなメ
リットが生じる.
のときのシンプソンの公式での積分値が計算できると言える.式
(19)のとおりである.しかし,式(18)を
直に計算する方法とどれほどのメリットがあるのだろうか?--という疑問も湧くだろう.
これだけだと,少し計算が早いかもしれないが,それほど大きなメリットはない.ただ,
台形公式と比べると,大変大きなメリットがある.台形公式とほとんど同じ計算で,シン
プソンの公式の精度が得られるのである.ロンバーグ積分まで考えると,さらに大きなメ
リットが生じる.
3.2.2 計算アルゴリズム
シンプソンの公式で数値積分を行う場合,式(18)を計算しても良いが, 台形公式を使う漸化式(19)を使うことを勧める.台形公式 からシンプソンの公式の値を求めるには,次のような手順で計算する.ただし,計算精度 は- 区間の区切りを
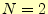 として台形公式で積分
として台形公式で積分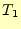 を計算する.計算結果は,
を計算する.計算結果は,
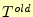 とする.
とする.
- 区間の区切りを
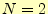 としてシンプソンの公式で積分
としてシンプソンの公式で積分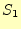 を計算する.計算結果
は
を計算する.計算結果
は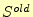 とする.
とする.
- 目的の精度に達するまで,以下を繰り返す.
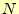 の値を2倍にする.それにともない,ステップ幅
の値を2倍にする.それにともない,ステップ幅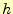 を半分にする.
を半分にする.
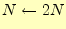
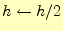
(20)
- 新しい台形公式の積分値を計算する.
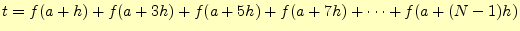
(21) 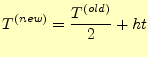
(22)
- 新しいシンプソンの公式の積分値を計算する.
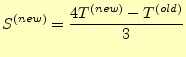
(23)
- 以下の条件を満たすならば,目的の計算精度に達したと判断して,繰り返
し文から脱出する.
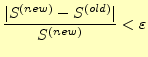
(24)
- 目的の精度に達していなければ,
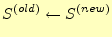
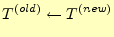
(25)
として,最初から繰り返す.
- シンプソンの公式による数値積分の結果
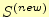 を表示する.
を表示する.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年1月19日
![\includegraphics[keepaspectratio, scale=1.0]{figure/simpson.eps}](img29.png)
![\begin{equation*}
% latex2html id marker 1155
\begin{aligned}\text{式(\ref{eq:si...
...i^2}{2}+2h^2\xi\right]_0^{2h}\\ &=\frac{h}{3}f(x_j) \end{aligned}\end{equation*}](img31.png)
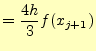
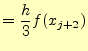
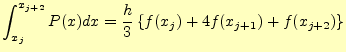
![\begin{equation*}\begin{aligned}S&=\frac{h}{3}\left[f(x_0)+4f(x_1)+f(x_2)\right]...
...}\left.\cdots+2f(x_{N-2})+4f(x_{N-1})+f(x_N)\right] \end{aligned}\end{equation*}](img42.png)
![$\displaystyle =h\left[ \frac{1}{2}f(a)+f(a+h)+f(a+2h)+f(a+3h)+f(a+4h)+\cdots+\frac{1}{2}f(a)f(a+Nh) \right]$](img51.png)
![$\displaystyle =h\left[ \frac{1}{3}f(a)+\frac{4}{3}f(a+h)+\frac{2}{3}f(a+2h)+\frac{4}{3}f(a+3h)+\frac{2}{3}f(a+4h)+\cdots+\frac{1}{3}f(a+Nh) \right]$](img53.png)
![\includegraphics[keepaspectratio,scale=1.0]{figure/trapezoid_simpson.eps}](img72.png)