2 簡単な回路の問題
2.1 CR直列回路
ここでは,常微分方程式の数値計算の練習問題として,図1に示す CR直列回路に流れる電流を求める.回路の問題なので,キルヒホッフの法則--回路の電 圧を一周に渡って積分するとゼロ--を使うのがセオリーで,それはとなる.電荷
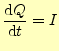 |
(2) |
となる.
式(1)を時間で微分して,電流と電荷の関係を用いると,
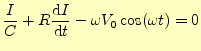 |
(3) |
という微分方程式が得られる.時刻が
![$\displaystyle I(t)=\frac{V_0\omega C\left[ \cos(\omega t)+R\omega C\sin(\omega t)-e^{-\frac{t}{CR}} \right]}{1+(R\omega C)^2}$](img7.png) |
(4) |
となる.ちょっとだけ面倒な式になっているが,気にすることはない.諸君は,複素関数 を使って,
今回の回路の問題では厳密解はあるが,練習を兼ねて数値計算で微分方程式を解いてみよ う.
2.2 数値計算
回路に流れる電流を時刻
0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
1.000000e-04 1.985456e-04 3.141593e-04 1.570021e-04 1.963076e-04
2.000000e-04 2.713744e-04 3.140042e-04 2.352707e-04 2.697098e-04
3.000000e-04 2.977589e-04 3.135393e-04 2.740179e-04 2.968290e-04
4.000000e-04 3.068621e-04 3.127650e-04 2.928500e-04 3.063989e-04
5.000000e-04 3.094132e-04 3.116820e-04 3.015707e-04 3.091954e-04
6.000000e-04 3.093600e-04 3.102914e-04 3.050827e-04 3.092600e-04
7.000000e-04 3.081557e-04 3.085946e-04 3.058380e-04 3.081095e-04
長いので,この辺は省略
9.995000e-01 3.084431e-04 3.085946e-04 3.082924e-04 3.084380e-04
9.996000e-01 3.101389e-04 3.102914e-04 3.099872e-04 3.101339e-04
9.997000e-01 3.115287e-04 3.116820e-04 3.113761e-04 3.115236e-04
9.998000e-01 3.126111e-04 3.127650e-04 3.124577e-04 3.126060e-04
9.999000e-01 3.133849e-04 3.135393e-04 3.132310e-04 3.133798e-04
1.000000e+00 3.138495e-04 3.140042e-04 3.136951e-04 3.138444e-04
さらに,厳密解との差--誤差--の絶対値のファイルも作成すること.第1列:時刻,第2列:オイラー
法の誤差,第3列:ホイン法の誤差,第4列:4次のルンゲ・クッタ法の誤差.![]() と
と![]() の値
をいろいろ計算してみよう.計算後さがどのようになるか調べてみよう.
の値
をいろいろ計算してみよう.計算後さがどのようになるか調べてみよう.
1.000000e-04 1.156137e-04 4.154344e-05 2.238011e-06
2.000000e-04 4.262985e-05 3.610366e-05 1.664613e-06
3.000000e-04 1.578046e-05 2.374101e-05 9.298990e-07
4.000000e-04 5.902889e-06 1.401218e-05 4.631933e-07
5.000000e-04 2.268803e-06 7.842526e-06 2.178372e-07
6.000000e-04 9.314720e-07 4.277303e-06 9.994238e-08
7.000000e-04 4.389742e-07 2.317686e-06 4.619756e-08
長いので,この辺は省略
9.992000e-01 1.478607e-07 1.467147e-07 4.904329e-09
9.993000e-01 1.492431e-07 1.481930e-07 4.952495e-09
9.994000e-01 1.504783e-07 1.495250e-07 4.995773e-09
9.995000e-01 1.515650e-07 1.507095e-07 5.034120e-09
9.996000e-01 1.525021e-07 1.517453e-07 5.067500e-09
9.997000e-01 1.532887e-07 1.526313e-07 5.095879e-09
9.998000e-01 1.539240e-07 1.533666e-07 5.119229e-09
9.999000e-01 1.544074e-07 1.539507e-07 5.137526e-09
1.000000e+00 1.547384e-07 1.543828e-07 5.150754e-09
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年10月2日
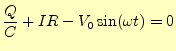
![\includegraphics[keepaspectratio, scale=1.0]{figure/RC_circuit.eps}](img9.png)