5 波動方程式
5.1 変数分離法
図6に示すようにこれを波動方程式と言う.ここで,
とそれぞれの変数の関数の積の形になると仮定する.これを変数分離形と言う.この仮定 した解を元の偏微分方程式に代入する.すると,
| (66) |
が得られる.これは,
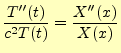 |
(67) |
となる.この左辺は時刻
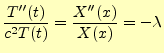 |
(68) |
となる.これを整理すると,
という連立常微分方程式になる.弦の振動の場合,図6に示すように 弦の両端で固定されている.固定されている部分では,弦の変位
| (71) |
である.この条件--境界条件--を満たすことができるのは,
である.時刻の項の常微分方程式(70)は,
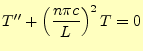 |
(73) |
となる.
となる.空間および時刻の常微分方程式から得られた解を元の仮定した解 (65)に代入すると
| (75) |
となる.元の波動方程式は線形なので,重ね合わせの原理が成り立つ.すなわち,解は
と書き表すことができる.
5.2 未知定数の値を決める
5.3 境界条件
弦の振動の境界条件は,| (77) |
である.物理的には,弦の両端を固定している--ことに対応している.すでに,この条 件は式(76)に含まれている.空間に関する波動方程式の解のうち
5.4 初期条件
式(76)のとする.この様子を図7と8に示 す.これらを初期条件という.初期の弦の形
偏微分方程式の解である式(76)が初期条件を満足するように![]() と
と
![]() を決めれば,波動方程式が完全に解けたことになる.それらの値は,初期条件と比
較することにより決めることができる.式(76)の
を決めれば,波動方程式が完全に解けたことになる.それらの値は,初期条件と比
較することにより決めることができる.式(76)の![]() の弦の形と速
度は,
の弦の形と速
度は,
| (80) | ||
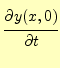 |
(81) |
となる6.
解の式から求めたこれらは,初期条件である式 (78)と(79)に等しい.だから,
となる.この式から,既知である
ここで,![]() と
と![]() を求める前に,
を求める前に,![]() と
と![]() の性質を考える.
の性質を考える.![]() や
や![]() の
定義域は
の
定義域は![]() である.したがって,
である.したがって,![]() や
や![]() はフーリエ級数,フーリエ正弦
級数,フーリエ余弦級数などで展開できる.また,
はフーリエ級数,フーリエ正弦
級数,フーリエ余弦級数などで展開できる.また,![]() と
と![]() で弦は固定されているので,
で弦は固定されているので,
| (84) | |
| (85) |
となる.これらのことから,
である.
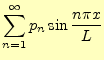 |
(88) | |
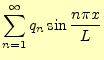 |
(89) |
となる.したがって,
| (90) |
である.これから,
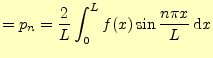 |
(91) | |
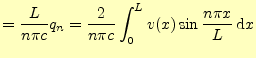 |
(92) |
と
5.5 具体的な弦の振動
弦の初期状態を図9のようにする.弦の中央をゆっくりとつま んで,そして離す.どのように振動するであろうか?
式(93)の![]() と
と![]() を決めれば,弦の振動は確定する.そのた
めに初期条件を考えよう.
を決めれば,弦の振動は確定する.そのた
めに初期条件を考えよう.![]() の時,弦の速度はどこでもゼロなので,
の時,弦の速度はどこでもゼロなので,![]() である.
したがって,式(87)より,
である.
したがって,式(87)より,
| (94) |
となる.残りの
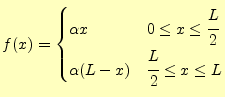 |
(95) |
と書くことができる.ここで,
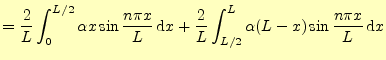 |
||
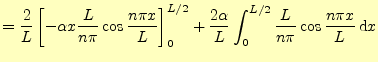 |
||
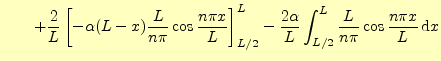 |
||
![$\displaystyle =-\frac{\alpha L}{n\pi}\cos\frac{n\pi}{2} +\frac{2\alpha}{L}\left...
...-\frac{2\alpha}{L}\left[\frac{L^2}{n^2\pi^2}\sin\frac{n\pi x}{L}\right]_{L/2}^L$](img282.png) |
||
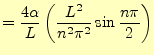 |
||
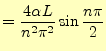 |
(96) |
![]() なので,弦の振動は,
なので,弦の振動は,
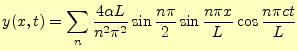 |
(97) |
となる.
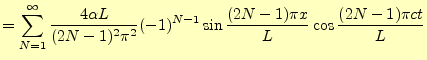 |
||
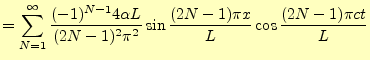 |
(98) |
となる.これが,最初の図9の状態の弦の振動を表す式である. これを弦の条件
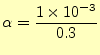 |
(99) |
を代入するとラの音がでる.位相が30度ごとの弦の状態を図10〜 15に示す.想像もつかないような弦の形になる.なぜ,このようなこ とが生じるか,物理的な理由を考えてみよ.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年2月28日
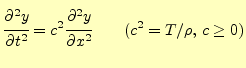
![\includegraphics[keepaspectratio, scale=1.0]{figure/string_vib.eps}](img174.png)
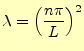
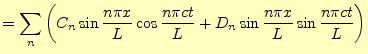
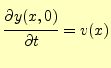
![\includegraphics[keepaspectratio, scale=0.8]{figure/string_vib_init_y.eps}](img211.png)
![\includegraphics[keepaspectratio, scale=0.8]{figure/string_vib_init_v.eps}](img216.png)
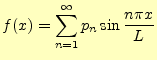
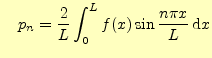
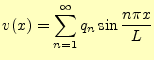
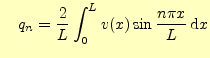
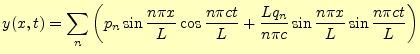
![\includegraphics[keepaspectratio, scale=1.0]{figure/string_triangle.eps}](img267.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/wave00.eps}](img298.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/wave30.eps}](img301.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/wave60.eps}](img304.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/wave90.eps}](img307.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/wave120.eps}](img310.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/wave150.eps}](img313.png)