6 ベクトル場の回転
次にベクトル演算子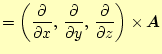 |
||
 |
||
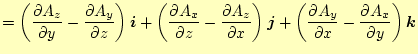 |
||
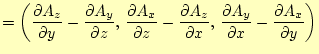 |
(18) |
となる。これは、回転と呼ばれるスカラー場である。ベクトル演算子とベクトル場のベク トル積なので、ベクトル量になると覚える。これが、実際にベクトル量になることの証明 は、諸君に任せる。
この量の物理的意味は、来週の積分の演算を通して示す。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 yamamoto masashi
平成17年5月14日
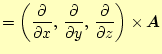 |
||
 |
||
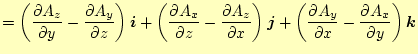 |
||
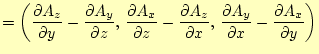 |
(18) |
この量の物理的意味は、来週の積分の演算を通して示す。