4 $\boldsymbol {\nabla }$演算子

ここでは、 $\boldsymbol {\nabla }$が演算子であり、ベクトルのような振る舞いを示すこと説明す る。式(11)から、

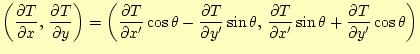$$\left( \if 11 \frac{\partial T}{\partial x} \else \frac{\partial^... ...prime} \else \frac{\partial^{1} T}{\partial y^\prime^{1}}\fi \cos\theta \right)$$ (13)

である。これを、

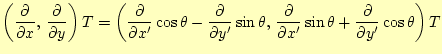$$\left( \if 11 \frac{\partial }{\partial x} \else \frac{\partial^{... ...prime} \else \frac{\partial^{1} }{\partial y^\prime^{1}}\fi \cos\theta \right)T$$ (14)

と書き改めても良いだろう。従って、 $(\partial/\partial x, \partial/\partial y, \partial/\partial z)$は演算子になっている。さらに、

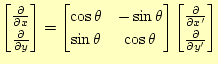$$\begin{bmatrix}\if 11 \frac{\partial }{\partial x} \else \frac{\p... ...al y^\prime} \else \frac{\partial^{1} }{\partial y^\prime^{1}}\fi \end{bmatrix}$$ (15)

の関係より、ベクトルのように振る舞うことが分かるだろう。

$\boldsymbol {\nabla }$を独立したベクトル演算子と考えると都合がよい。どのように都合が良い かは後で述べる。勾配を表す式(6)では $\boldsymbol{\nabla} T$ で一つの記号で あったが、今後はベクトル演算子 $\boldsymbol {\nabla }$ スカラー場 $T$ との積と考える。すな わち、

$$\boldsymbol{\nabla}T =\left( \if 11 \frac{\partial }{\partial x} \else \frac{\partial^... ...c{\partial }{\partial z} \else \frac{\partial^{1} }{\partial z^{1}}\fi \right)T$$

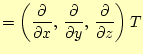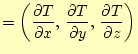$$=\left( \if 11 \frac{\partial T}{\partial x} \else \frac{\partial... ...{\partial T}{\partial z} \else \frac{\partial^{1} T}{\partial z^{1}}\fi \right)$$ (16)

である。ベクトル演算子 $\boldsymbol {\nabla }$ は右側にある量に作用することを忘れてはなら ない。従って、積の交換法則は成り立たず、 $\boldsymbol{\nabla}T\neq T\boldsymbol{\nabla}$ である。

また、これは微分を表すことも忘れてはならない。微分演算子 $\mathrm{d}/\mathrm{d}x$ のようにである。このベクトル演算子はは当然スカラー場やベクトル量に作用する。

ベクトル演算子はベクトル量とスカラー積やベクトル積をとることができる。それについ ては、次節以降に述べる。

ホームページ: Yamamoto's laboratory
著者: 山本昌志