5 付録
5.1 回転を表す行列について
回転を表す行列の性質を調べる。後々の都合を考えて、カーテシアン座標系をと表すことができる。これをいちいち成分で書かずに、
回転を表す行列の成分![]() は、
は、![]() 軸と
軸と![]() 軸の方向余弦を表している。これ
は、2次元の回転を考えれば簡単に分かる。2次元の回転は、
軸の方向余弦を表している。これ
は、2次元の回転を考えれば簡単に分かる。2次元の回転は、
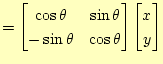 |
||
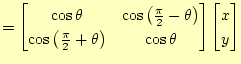 |
(23) |
となる。これと、図6から、回転を表す行列の成分は軸の方向余弦 であることが分かる。方向余弦はその方向の成分を表すのであるから当然であろう。
これらのことから、![]() はプライムがつく
はプライムがつく![]() 軸とプライムが付かない
軸とプライムが付かない![]() 軸の方向余
弦を表す。従って、
軸の方向余
弦を表す。従って、
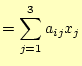 |
(24) | |
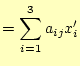 |
(25) |
となる。これらの式のうち、前者は式(22)を表す。後者の式は、
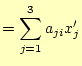 |
(26) |
となる。回転の行列が転置行列になっていることが分かるであろう。すなわち、
 |
(27) |
である。これらのことから、座標軸が回転した場合の座標やベクトルの変換は簡単に表す ことができる。すなわち、
| (28) | ||
| (29) |
のようにである。
これらの式を比べると、重要な結果
| (30) |
が得られる。
- [練習1]
- 2次元カーテシアン座標系の回転を表す行列の逆行列を求め よ。
- [練習2]
- その逆行列は、元の行列の転置行列になっていることを示 せ。。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 yamamoto masashi
平成17年5月14日

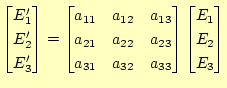
![\includegraphics[keepaspectratio, scale=1.0]{figure/rot_two_dim.eps}](img101.png)