5 ベクトルの別の表現

5.1 成分を用いた表現

これまでの話で、ベクトルは矢で表されることが分かった。矢で表すと直感的に分かり易 いが、計算には不向きである。そこで、別の表現を考えることにする。図 7のようにその矢の始まりをカーテシアン ²座標系の原点におい て、先端の座標で表すことができる。そうすると、位置ベクトル $\boldsymbol{r}$の場合、

$$\boldsymbol{r}_1=(x_1,y_1,z_1)$$ (3)

のような表現が可能であろう。この、 $x_1, y_2, z_3$をベクトル $\boldsymbol{r}$の成分、あ るいは射影と言う。我々は3次元(相対論では4次元)の世界に住んでいるので、物理学で取 り扱うベクトル量は3つの成分からなる。

図 7: カーテシアン座標系をつかったベクトルの表現

このようにすると、ベクトルの表現は全く便利になる。今までの矢を用いた方法だと、ベ クトル量の計算が大変やっかいである。計算するとなると数値で表すことになるが、長さ と角度みたいな量で表すことになる。2つのベクトル量をそれぞれ長さと角度の数値

$$\boldsymbol{A}=(r_A, \theta_A)$$ (4)

$$\boldsymbol{B}=(r_B, \theta_B)$$ (5)

で表現したとする³。これを加算することを考えると、かなり面倒 である。

$$\boldsymbol{C} =\boldsymbol{A}+\boldsymbol{B}$$

$$=( , )$$ (6)

一方、座長を用いた表現だと

$$\boldsymbol{C} =\boldsymbol{A}+\boldsymbol{B}$$

$$=(A_x, A_y, A_z)+(B_x,B_y,B_z)$$ (7)

$$=(A_x+B_x, A_y+B_y, A_z+B_z)$$ (8)

のように簡単に演算ができる。成分同士を加算すれば良いのである。これは、まったくもっ て便利である!!!!。

ここで、先ほどのカーテシアン座標の各軸に沿った単位ベクトルを導入すると、便利な場 合がある。図8のようにすると、

$$\boldsymbol{A} =(A_x, A_y, A_z)$$

$$=A_x\boldsymbol{i}+A_y\boldsymbol{j}+A_z\boldsymbol{k}$$ (9)

のように表現できる。ここで、 $\boldsymbol{i}$, $\boldsymbol{j}$, $\boldsymbol{k}$が各軸に沿った単位ベクト ルである。

成分を使った表現では、ベクトルの大きさも簡単に計算でき、ピタゴラスの定理より

$$\vert\boldsymbol{A}\vert=A_x^2+A_y^2+A_z^2$$ (10)

となる。

図 8: 単位ベクトル

[練習1]

2つのベクトル

$$\boldsymbol{A}=(1,2,3)$$

$$\boldsymbol{B}=(3,2,1)$$

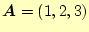
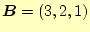
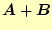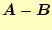の $\boldsymbol{A}+\boldsymbol{B}$と $\boldsymbol{A}-\boldsymbol{B}$を示せ。

[練習2]

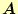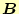[練習1]のベクトル $\boldsymbol{A}$と $\boldsymbol{B}$の大きさを示せ。

5.2 方向余弦について

後に、方向余弦と言う話も出てくるので、少し説明をしておく。図 7に示したように成分を使って、ベクトルは表現可能である。 ベクトルの大きさを$r$として、各軸との角度をそれぞれ図9のよ うにすると、

$$r_x=r\cos\alpha r_y=r\cos\beta r_z=r\cos\gamma$$ (11)

の関係がある。ここで、$r$はベクトル $\boldsymbol{r}$の大きさを表す。これらの $r\cos\alpha, r\cos\beta, r\cos\gamma$を方向余弦と言う。

図 9: 方向余弦

ホームページ: Yamamoto's laboratory
著者: 山本昌志