2 電流にはたらく力
2.1 直線電流に働く力
無限に長い直線電流どうしに働く力を考える。そのために、それが作る磁場を計算する。 磁場は微分形のアンペールの法則| (1) |
から導くのが簡単である。磁束密度
| (2) |
の関係がある。これを用いると、
| (3) |
となる。この直線電流から、
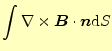 |
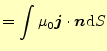 |
|
| 左辺にストークスの定理を応用すると | ||
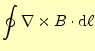 |
||
| (4) |
これから、磁束密度は
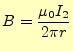 |
(5) |
となる。この磁束密度は元々、力から定義されていた。図 1のように置かれた電線が単位長さ当たり受ける力は、
となる。
式(6)に示した力は平行に導線を張った場合に働く力で ある。それに対して、平行でない場合は、
| (7) |
となる。これをアンペールの力と言う。
2.2 長方形コイルに働く力
教科書の図6.2に書いてある通り、コイルの上下方向の力は、反対で一直線上にある。し たがって、コイルの重心を移動させる力は発生しない。トルクはどうだろうか?。ゼロで あることは直ちに理解できる。上下方向の力をそれぞれ、| (8) |
となる。直感の通り、ちゃんと計算してもコイルの上下方向の働くトルクは、キャンセルされ る。
左右方向はどうだろうか?。力の大きさが反対なので、重心を移動させる力は発生しない。
しかし、トルクは発生する。左右方向の力をそれぞれ、
![]() と
と
![]() とすると
とすると
| (9) |
となる。ここで、
| (10) |
となる。方向は、コイルの左右の線と力との双方に垂直な方向である。また、力はアンペー ルの法則より、
| (11) |
となる。ここで、
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月24日
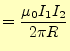
![\includegraphics[keepaspectratio, scale=1.0]{figure/Ampere_force_two_wire.eps}](img18.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/Ampere_force_current_element.eps}](img19.png)