2 ビオ-サバールの法則
2.1 ビオ-サバールの法則
静電場の場合、微少体積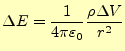 |
(1) |
となった。これに対応する静磁場の式がビオ-サバールの法則である。電流
となる。図1にこれらの位置関係を示す。この微小磁場
- 大きさは、式(2)の示すとおりである。
- 観測点の位置ベクトル
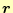 と微少電流ベクトル
と微少電流ベクトル
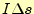 の
両方に垂直な方向を向いている。
の
両方に垂直な方向を向いている。
ちょっとこれらの式は方向を指定することが不可能なので、それを含めた正確なベクトル で表現する。ベクトルを用いて表現すると、図など書かなくても式が全てを語っている。それぞれは、
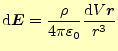 |
(3) | |
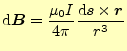 |
(4) |
となる。ただし、微少電流や微少電荷を座標原点に置いている。この後者をビオ-サバー ルの法則と言う。
後者の式は、
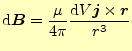 |
(5) |
と書いた方が電場の式との対応が良い。こうなると、
2.2 ビオ-サバールの法則の導出
このビオ-サバールの法則は、特殊相対性理論を用いて導くのが本来の姿と思われるが、 そこまですると、講義の時間が不足する。そこで、静磁場の知識のみですむ教科書と同じ 説明をする。正直に言うと、このような説明方法があるとは知らなかった。さすが、砂川 重信先生である。今まで学習してきた磁場は、全て端が無い電流により作られる。すなわち、無限に長い電 線や閉じた電線である。ビオサバールの法則を見ると、微少区間の電流を取り扱っている ので、端が存在する。そのような電流を考えると、積分型のアンペールの法則が成り立た なくなる。これは、電流が保存されていないからである。
電流が保存された系で微少電流を考えるために、教科書では、微少電線の両端で発散と収 束を考えている。このようにする限り、電流は保存され、積分型のアンペールの法則が成 立する。また、これらの微少電流を足しあわせることにより、無限に長い電流や閉じた電 流を考えることができる。この辺の所は教科書の図の通り。
それでは、このような微少電流からビオ-サバールの法則が成立するか、調べることにす
る。教科書の図5.9(a)に示している磁場
![]() を求める。そのために、積分形
のアンペールの法則
を求める。そのために、積分形
のアンペールの法則
を使う。ある閉じた面の縁の磁場の線積分は、内部の電流密度の面積分に等しい。もっと 簡単に言うと、磁場を線積分したら、そこの面を流れる電流に等しいと言っているのであ る。これを利用して磁場を求めようと言うのである。ビオ-サバールの法則を考えるため に、積分を行う範囲は、教科書の通り、円の一部を切り取った範 囲が適当である。この部分では、電流は一定である。なぜならば、微少電線の端では、球状に電 流が発散及び収束しており、この部分球の表面はその端から等距離にある。従って、ここ での電流密度は、
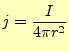 |
(7) |
となる。また、対称性から、磁場の大きさも一定
アンペールの法則、式(6)を用いて磁場![]() を計算することにな
るが、この左辺は簡単で
を計算することにな
るが、この左辺は簡単で
となる。
次に、式(6)の右辺を考えることにする。この右辺は、積分領域の
電流のを表している。ここでの、積分を行う部分の電流密度は一定で、
![]() と分かっている。したがって、積分領域の面積さえ分かれば、電流は計算でき、右
辺の値が分かることになる。教科書の図5.9(b)の帯状の微少区間の面積は、
と分かっている。したがって、積分領域の面積さえ分かれば、電流は計算でき、右
辺の値が分かることになる。教科書の図5.9(b)の帯状の微少区間の面積は、
| (9) |
となる。従って全ての面積は、区間
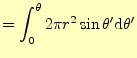 |
||
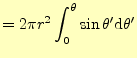 |
||
| (10) |
と求められる。従って、微少電線のAから流出する電流の総量は、この面積に電流密度を かければ求められ、
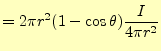 |
||
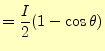 |
(11) |
となる。これは、距離に関係なく、角度のみに依存する。電流は保存され、球状に放出さ れるので当たり前のことである。
次に、同じ縁を持つ積分領域で教科書の図5.9のB点から吸収される電流を計算する。先の A点の放出電流の式が使える。異なるところは、角度のみである。したがって、B点への吸 収電流はとなる。
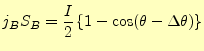 |
(12) |
A点の放出電流と、B点の吸収電流をあわせたものがトータルの電流で、
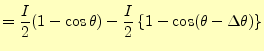 |
||
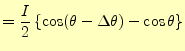 |
||
|
|
||
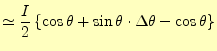 |
||
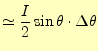 |
(13) |
となる。したがって、円
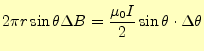 |
(14) |
となる。したがって、微小磁場は
となる。ビオ-サバールの法則まで、後一歩である。そのためには、
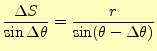 |
(16) |
から、
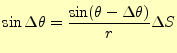 |
(17) |
が導かれる。
となる。
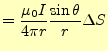 |
||
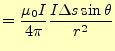 |
(19) |
となる。これがビオ-サバールの法則である。微少電流が作る微小磁場を表している。
もっと一般的な座標で書くと、
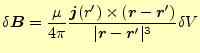 |
(20) |
となる。ここで、
2.3 円電流が作る静磁場
問題のコイルの1個が軸上に作る磁場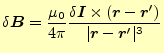 |
(21) |
から計算できる。これから、その磁場は図5 の右の絵のようになる。軸上の磁場
図から分かるように、微小磁場
![]() は軸の垂直成分もある。しかし、
これは、コイル1週にわたって足し合わせると、ゼロになる。コイル1周にわたっ
て合計すると、残るのは軸上の成分のみである。コイルの軸上の成分は、
は軸の垂直成分もある。しかし、
これは、コイル1週にわたって足し合わせると、ゼロになる。コイル1周にわたっ
て合計すると、残るのは軸上の成分のみである。コイルの軸上の成分は、
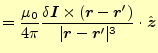 |
||
|
|
||
|
|
||
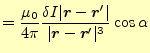 |
||
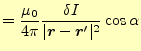 |
||
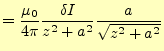 |
||
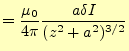 |
(22) |
となる。これをコイルの全ての電流で積分することになるが、
となる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月24日
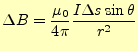
![\includegraphics[keepaspectratio, scale=1.0]{figure/BiotSavart_coil.eps}](img9.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/dI_conserv_current.eps}](img14.png)
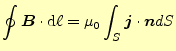
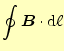
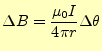
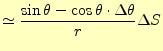
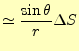
![\includegraphics[keepaspectratio, scale=1.0]{figure/theorem_sin.eps}](img56.png)
![\includegraphics[keepaspectratio, scale=0.8]{figure/dB_by_dj.eps}](img60.png)
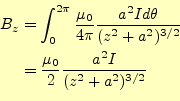
![\includegraphics[keepaspectratio, scale=1.0]{figure/OneTurn_coil.eps}](img79.png)