Subsections
2 差分法による1次元波動方程式の数値計算
このあたりの説明は,参考文献 [1]を大いに参考にした.これは分 かりやすい教科書なので,読んでみると良いだろう.2.1 差分方程式
1次元波動方程式を数値計で解くことを考える.その前に,解くべき方程式と条件をきち んと書いておく.解くべき方程式と条件は,となる.弦を伝わる波の速度は1,弦の長さも1としている.この最初の式は波動方程式で あるが,2番目を初期条件,3番目を境界条件と言う.2番目の初期条件は,
波動方程式の他に,初期条件と境界条件がある.力学的状態は,ある時刻,ここでは
![]() の時の変位とその変位の速度が決まれば,それ以降を決めることができる.振動の
場合は,これに加えて更に,振動の境界条件を決める必要がある.これらが決まって初め
て,波動方程式とともに,振動の状態,ある時刻と位置の変位の値が決まるわけである.
図4に初期条件と境界条件の様子を示す.
の時の変位とその変位の速度が決まれば,それ以降を決めることができる.振動の
場合は,これに加えて更に,振動の境界条件を決める必要がある.これらが決まって初め
て,波動方程式とともに,振動の状態,ある時刻と位置の変位の値が決まるわけである.
図4に初期条件と境界条件の様子を示す.
まずは,波動方程式を差分方程式に書き直すことからはじめる.これも,いつものように,
解![]() をテイラー展開する.x方向の微小変位を
をテイラー展開する.x方向の微小変位を![]() ,時間軸方向の微小変位
を
,時間軸方向の微小変位
を![]() とする.すると,
とする.すると,
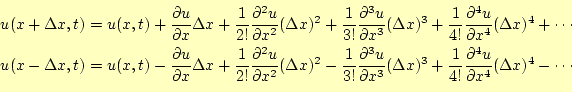 |
となる.これらの式の辺々を足し合わせえると,
が得られる.このことから,2階の偏導関数の値は微小変位
が得られる.
これらの式(6)と(7)を元の波動 方程式(4)に代入すれば,
となる.これが,1次元波動方程式の差分の式である.この式を計算し易いように,もう 少し変形すると,
とすることができる.この式の右辺は,時刻
実際に式(9)を数値計算する場合,x方向には![]() ,時間軸方向には
,時間軸方向には
![]() 毎に分割する.ラプラス方程式を格子点で分割したのと同じである.格子点に
分割し数値計算する場合,
毎に分割する.ラプラス方程式を格子点で分割したのと同じである.格子点に
分割し数値計算する場合,![]() や
や
![]() と表現するよりは,
と表現するよりは,![]() と表現したほうが便利である.そこで,
と表現したほうが便利である.そこで,
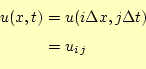 |
と表現を改める.このようにすると,式(9)は
となり,数値計算し易い形になる.ただし,
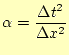 |
(12) |
である.
この式を用いた計算の様子を図3に示す.
波動方程式というけったいな偏微分方程式が,ただ単に数値を順番に代入していく式に変
換されたわけである.この計算は非常に簡単である.ただ,時間領域を1000分割
(![]() ),x軸領域も1000分割(
),x軸領域も1000分割(![]() )すると,100万回の計算が必要であるが,
コンピューターにとって,その程度の計算は大したことはない.
)すると,100万回の計算が必要であるが,
コンピューターにとって,その程度の計算は大したことはない.
2.2 初期条件
式(11)を計算すると,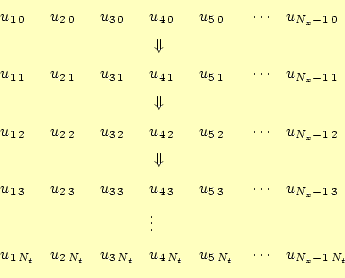 |
このように,計算を盲目的に進めれば,弦の振動の式(4) の数値計算の結果である近似解が得られる.当然,境界条件
| (13) |
を,忘れてはならない.
これを計算するためには,まず,
![]() の値を決める
必要がある.これ以前の状態が分からないので,式(11)は使えないが,式
(4)の初期条件が使える.すなわち,
の値を決める
必要がある.これ以前の状態が分からないので,式(11)は使えないが,式
(4)の初期条件が使える.すなわち,
| (14) |
である.
次に,
![]() を計算するわけであるが,まだ,式
(11)は使えない.なぜならば,この式は2つ前の状態まで必要なので,こ
れまでのところ,一つ前の状態しか分かっていないからである.そこで,2番目の初期条
件(変位の速度)を使うことになる.計算したい量は
を計算するわけであるが,まだ,式
(11)は使えない.なぜならば,この式は2つ前の状態まで必要なので,こ
れまでのところ,一つ前の状態しか分かっていないからである.そこで,2番目の初期条
件(変位の速度)を使うことになる.計算したい量は
![]() なので,とりあえず
テーラー展開してみる.これを,
なので,とりあえず
テーラー展開してみる.これを,![]() の周りでテーラー展開すると,
の周りでテーラー展開すると,
 |
となる.この右辺の第1と2項は簡単に計算できる.問題は第3項であるが,これは見覚え のある式である.式(6)と同じである.これを代入すると,
![\begin{equation*}\begin{aligned}%
u(x,\Delta t) %
&\thickapprox u(x,0) +\psi(x...
...[ u(x+\Delta x,t)-2u(x,t)+u(x-\Delta x,t)\right] %
\end{aligned}\end{equation*}](img44.png) |
となる.これは,めでたい式である.右辺は,
| (17) |
が得られる.
以上より,![]() と
と![]() が得られたわけである.
が得られたわけである.![]() 以降は,
式(11)に従い,計算すればよい.
以降は,
式(11)に従い,計算すればよい.
2.3 進行波の取り扱い
今までの議論で定在波の取り扱いは可能であろう.そこで,進行波の記述方法について, コメントしておく.進行波を数値計算すると面白いのでその方法を示す.進行波を記述す るためには,初期条件さえ記述すれば,後の差分方程式は同じである.その初期条件の記 述の仕方を示す.元の波動方程式
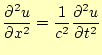 |
(18) |
には,明らかに,ダランベールの解
| (19) |
というものがある.これは元の波動方程式に代入すれば,それを満足していることは直ち に理解できる.ここで,
初期条件
の波がx軸を正の方向に進む進行波として取り扱うには,どうしたらよいだろうか?.のこ る条件は,
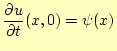 |
(21) |
である.進行波になるように,
となる.この式を使って,
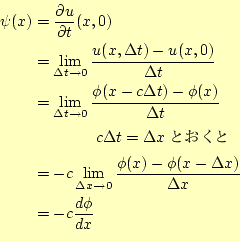 |
となる.進行波にするためには,
念のため言っておくが,後進波にするためには
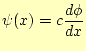 |
(24) |
とすればよい.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
2006-02-07
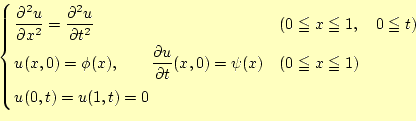
![\includegraphics[keepaspectratio, scale=0.85]{figure/wave_init.eps}](img14.png)
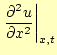
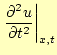
![$\displaystyle u(x,t+\Delta t)= 2u(x,t)-u(x,t-\Delta t)+ \frac{\Delta t^2}{\Delta x^2}\left[ u(x+\Delta x,t)-2u(x,t)+u(x-\Delta x,t) \right]$](img25.png)
![\includegraphics[keepaspectratio, scale=0.85]{figure/sabun.eps}](img34.png)