3 二分法(bisection method)

3.1 計算方法

二分法の原理は非常に単純であるが、この方法は場合によっては非常に強力である。これ は、閉区間$[a,\,b]$で連続な関数$f(x)$の値が、

$$f(a)f(b)<0$$ (7)

ならば、 $f(\alpha)=0$となる$\alpha$が区間$[a,\,b]$ということを使っている。このこ とは、中間値の定理から保証されるが、常識的に考えてあたりまえである。ただ、連続な 区間で適用できることを忘れてはならない。

実際の数値計算は、 $f(a)f(b)<0$であるような2点 $a,\,b(a<b)$から出発する。そして、 区間$[a,\,b]$を2分する点$c=(a+b)/2$に対して、$f(c)$を計算を行う。 $f(c)f(a)<0$な らば$b$を$c$と置き換え、 $f(c)f(a)>0$ならば$a$を$c$と置き換える。絶えず、区間 $[a,b]$の間に解があるようにするのである。この操作を繰り返して、区間の幅$\vert b-a\vert$が 与えられた値 $\varepsilon$ よりも小さくなったならば、計算を終了する。解へ収束は収 束率1/2の一次収束となる。

実際にこの方法で式(2)を計算した結果を図 2に示す。この図より、$f(a)$と$f(b)$の関係の式 (7)を満たす区間$[a, b]$が1/2ずつ縮小していく様子がわかる。この方法 の長所と短所は、以下の通りである。

長所

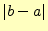閉区間$[a,b]$に解があれば、必ず解に収束する。間違いなく解を探すので、 ロバスト(robust：強靭な)な解法と言われている。次に示すニュートン法と は異なり、連続であればどんな形の関数でも解に収束するので信頼性が高い のである。さらに、解の精度も分かり便利である。解の誤差は、区間の 幅$\vert b-a\vert$以下である。

短所

収束が遅い(図8)。

図 2: $f(x)=x^3-3x^2+9x-8$の実数解を二分法で解散し、その解の収束の 様子を示している。初期値は $a=-1,\,b=11$として、最初の解$c=x_0=5$が求 まり、順次より精度の良い $x_1,\,x_2,\,x_3,\cdots$が求まる。それが、解析解 $x=1.1659\cdots$(x軸との交点)に収束していく様子が分かる。

3.2 フローチャート

関数はあらかじめ、プログラム中に書くものとする。更に、計算を打ち切る条件もプログ ラム中に書くものとする。そうすると、図3のような二分法の フローチャートが考えられる。

図 3: 二分法のフローチャート

ホームページ: Yamamoto's laboratory
著者: 山本昌志