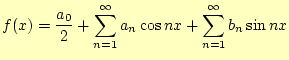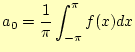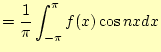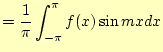Subsections
1 フーリエ級数
連立方程式の最後の問題は,フーリエ級数に関係した問題です.そこで,その問題につい て簡単に解説しておく.1.1 フーリエ級数とは
フーリエ級数は,フーリエ(1768-1830 フランス)が熱伝導の方程式を研究しているときに 発見した級数です.今は,もっぱら波(振動も波と考える)の問題に適用されています.
フーリエ級数とは,つぎのように区間[![]() ]で定義された任意の関数を
]で定義された任意の関数を![]() と
と
![]() で展開したものです.
で展開したものです.
この式が正確に成り立つために
このように関数を展開することはいろいろな場面で使われます.皆さんは,フーリエ級数 以外にも冪乗に展開するテイラー展開というものをすでに学習しているはずです.場面に 応じて都合の良い展開を使えばよいのです.
本当に任意の関数が,式(1)に展開できることの証明は数学
の教科書に譲ることにして,その展開の係数,フーリエ係数![]() と
と![]() を求める方法
を示します.これこそが,フーリエ級数やフーリエ変換,あるいはコンピューターによる
離散フーリエ変換(DFT)または高速フーリエ変換(FFT)の実際の計算です.
を求める方法
を示します.これこそが,フーリエ級数やフーリエ変換,あるいはコンピューターによる
離散フーリエ変換(DFT)または高速フーリエ変換(FFT)の実際の計算です.
この展開係数の理論的な式は,三角関数の次の性質を使いことにより求めることができま
す.ただし,![]() と
と![]() は1以上の整数とします.
は1以上の整数とします.
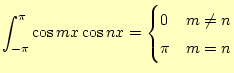 |
(2) |
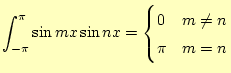 |
(3) |
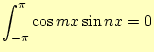 |
(4) |
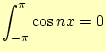 |
(5) |
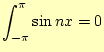 |
(6) |
まずは,
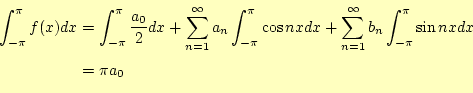 |
となります.これから,
と計算できます.
つぎに,![]() を求めよう.式(1)の両辺に
を求めよう.式(1)の両辺に![]() を書けて,区間[
を書けて,区間[![]() ]を
]を![]() で積分します.すると,
で積分します.すると,
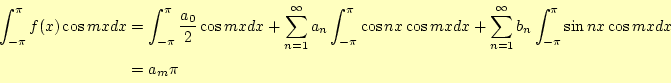 |
となります.これから,直ちに
となります.ここで,この式と式(8)を比べます.すると,
となることが分かります.式がひとつ節約できたことになります.同様に,
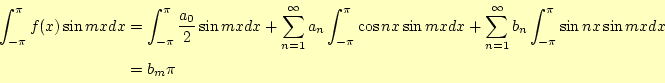 |
となります.したがって,
と求めることができます.この式と式(11)からフーリエ係数 が計算でき,式(1)の展開が可能となるわけです.
これまでは,関数の区間[![]() ]としてきましたが,式
(1)はその区間の外側でも計算できます.外側の
値が気になるところですが,これは三角関数の性質により直ちにわかります.
フーリエ級数を形成する三角関数は,
]としてきましたが,式
(1)はその区間の外側でも計算できます.外側の
値が気になるところですが,これは三角関数の性質により直ちにわかります.
フーリエ級数を形成する三角関数は,![]() の周期を持ちますので,フーリエ
級数も同じ周期を持つことになります.したがって,区間[
の周期を持ちますので,フーリエ
級数も同じ周期を持つことになります.したがって,区間[![]() ]の形が
その外側で周期的に現れることになります.波と一緒です.
]の形が
その外側で周期的に現れることになります.波と一緒です.
1.2 対称性
フーリエ級数は,あらゆる関数は三角関数からできていると言っています.その三角関数 は,原点をを境に対称な
もし,元の関数が原点を境に対象な形をしているならば,そのフーリエ級数は![]() の和のみで書かれることになります2.一方,原点を中心に反対照な関数であれば,
の和のみで書かれることになります2.一方,原点を中心に反対照な関数であれば,![]() の和のみで表現できます.
これは,
の和のみで表現できます.
これは,![]() や
や![]() を求める式からも理解できます.
を求める式からも理解できます.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
2005-11-25