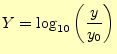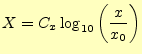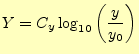2 方眼紙について

諸君が使う方眼紙は，普通の方眼紙(名前??),型対数方眼紙，両対数方眼紙が主である． これらをデータに応じて使い分ける必要がある．まず，これらの方眼紙の特徴を述べる．

2.1 普通の方眼紙

これは，もっともおなじみの，x軸とy軸ともリニアーになっているものである．説明する までもなく，よく知っているだろう．これはグラフ上の基準点からの距離($X, Y$)に，デー タ$(x,y)$を

$$X=C_{0x}+C_{1x}x Y=C_{0y}+C_{2y}y$$ (1)

のようにプロットする．$C_{1x}$と$C_{1y}$はグラフのスケールを決める定数，$C_{0x}$ と$C_{0y}$はオフセットである．難しいことを言わなくても，x軸とy軸の交点(基準点)を $(C_{0x},C_{0y})$として，等間隔に目盛りを付けていると言うだけのことである．

したがって，x軸とy軸ともリニアーになっている方眼紙では，$y=ax+b$の一次関数が

$$\frac{\mathrm{d}Y}{\mathrm{d}X} =\frac{C_{1y}}{C_{1x}}\frac{\mathrm{d}y}{\mathrm{d}x}$$

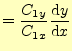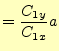$$=\frac{C_{1y}}{C_{1x}}a$$ (2)

のように，グラフ用紙で直線になる．なぜならば，$x$に依存しないで，傾きが一定となっ ているからである．このグラフの傾き $\mathrm{d}Y/\mathrm{d}X$と，スケールの比$C_2/C_1$から，デー タの1次関数の係数$a$が分かるのである．

2.2 片対数方眼紙

この方眼紙の軸は，ちょっと変わっていて，片方はリニアーで，もう一方は対数軸がであ る．横軸，縦軸のいずれも対数軸にすることができるが，ここでは話を簡単にするために，縦軸を対 数軸とする．そうすると，横軸はリニアー軸になる．先ほどと同様にグラフ上の基準点か らの距離を$(X,Y)$とする．この場合は，

$$X=C_{0x}+C_{1x}x Y=C_{1y}\log_{10}\left(\frac{y}{y_0}\right)$$ (3)

となる．$C_{1x}$と$C_{1y}$はグラフのスケールを決める定数である．$C_{1y}$は1にす るのが普通である．以降，$C_{1y}=1$として話を進める．$C_{0x}$ は，x軸のオフセット である．$y_0$は基準点($Y=0$)での，yの値である．もう一度ちゃんと書くと，データは，

$$X=C_{0x}+C_{1x}x Y=\log_{10}\left(\frac{y}{y_0}\right)$$ (4)

と片対数方眼紙でプロットされる．

このグラフでは，指数関数

$$y=ab^{cx}$$ (5)

が直線になる．これは，

$$y=ae^{xc\log_eb}=a10^{xc\log_{10}b}$$ (6)

から，底が$e$や$10$でもおなじことである．一般に，片対数方眼紙は，指数が10の時， 便利に使えるように考慮されている．と思っていたら，今回，捜してきた片対数グラフは そうなっていない．非常に驚いたが，近頃はそういうのもあるらしい．ここでは，昔から 使われてきた，横軸の10目盛り(10cm)の寸法と縦軸の1桁が10cmと等しいものを対象にす る．

そこで，

$$y=\alpha 10^{\beta x}$$ (7)

がどのように表されるか，考える．式(4)より，

$$\mathrm{d}X=C_{1x}\mathrm{d}x$$ (8)

となる．一方， $\mathrm{d}Y$は，式(7)を式(4)に代入して 計算すればよく，

$$\mathrm{d}Y=\beta \mathrm{d}x$$ (9)

となる．したがって，グラフ上の傾きは，

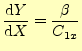$$\frac{\mathrm{d}Y}{\mathrm{d}X}=\frac{\beta}{C_{1x}}$$ (10)

となる．これから，片対数方眼紙では，指数関数が直線で表せることが分かった．そして， その傾きは， $\beta/C_{1x}$を表し，$\beta$が容易に求まることが分かった．

2.3 両対数方眼紙

このグラフは，片対数方眼紙と同じように考えることができ，データ$(x,y)$は，グラフ 上の$(X,Y)$

$$X=C_x\log_{10}\left(\frac{x}{x_0}\right) Y=C_y\log_{10}\left(\frac{y}{y_0}\right)$$ (11)

に変換される．

この方眼紙は，

$$y^{\alpha}=Cx^{\beta}$$ (12)

が直線になる．このことを，今までと同じように確認してみよう．まずは，式 (11)から，

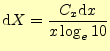$$\mathrm{d}X=\frac{C_x\mathrm{d}x}{x\log_e10}$$ (13)

となる．次に， $\mathrm{d}Y$であるが，

$$y=C^{1/\alpha}x^{\beta/\alpha}$$ (14)

と変形しておく．これを，式(11)に代入して，整理すると，

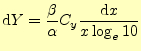$$\mathrm{d}Y=\frac{\beta}{\alpha}C_y\frac{\mathrm{d}x}{x\log_e10}$$ (15)

となる．したがって，グラフ上の傾きは，

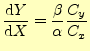$$\frac{\mathrm{d}Y}{\mathrm{d}X}=\frac{\beta}{\alpha}\frac{C_y}{C_x}$$ (16)

となり，いつも一定で直線になる．

通常，両対数方眼紙は，$C_y/C_x=1$になるように作られるので，グラフの傾きは $\beta/\alpha$をあらわす．

ホームページ: Yamamoto's laboratory
著者: 山本昌志