1.2 原理
1.2.1 共振回路
図1.1のようなLCR直列共振回路に交流電圧Eを加えた とき、回路に流れる電流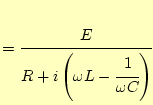 |
(1.1) |
となり、その大きさは
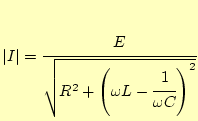 |
(1.2) |
とである。
いま、電流が最大に流れるように、交流電源の角振動数![]() を調整して、
を調整して、
![]() とする。すなわち、
とする。すなわち、
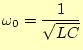 |
(1.3) |
とする。
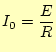 |
(1.4) |
となる。最大の電流が流れるこの状態を共振と言う。丁度、電源の周波数と回路の固有振 動数が一致している状態となっている。図1.1のよう な回路を直列では直列共振という。そして、電源の電圧を一定にしてその周波数を変化さ せると、図1.2のように回路に流れる電流が変わる。 このような図を共振曲線という。
図から明らかなように、![]() の小さい回路では共振時の電流
の小さい回路では共振時の電流![]() は非常に大きくなるが、
共振周波数からずれると、それは急激に減少する。この共振曲線の形状の鋭さを測る物差
しとして
は非常に大きくなるが、
共振周波数からずれると、それは急激に減少する。この共振曲線の形状の鋭さを測る物差
しとして![]() を定義し、これを共振の鋭さ(sharpness of resonance)と言う。
を定義し、これを共振の鋭さ(sharpness of resonance)と言う。
![]() が
が![]() の
の
![]() になる周波数を
になる周波数を
![]() 、
、
![]() として、
として、
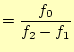 |
||
| (1.5) |
と定義する。
1.2.2 Q値の測定方法
ここでは、周波数を一定にして、コンデンサーの容量を変化させた場合の電流を測定して、 Q値を求める。図1.1の回路では、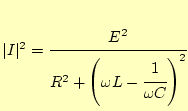 |
(1.6) |
となる。ところで、共振時にはこの式の分母の括弧の中がゼロとなるので、
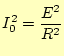 |
(1.7) |
である。これより、
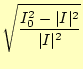 |
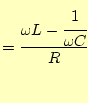 |
|
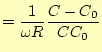 |
||
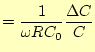 |
(1.8) |
ここで、
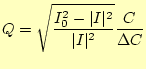 |
(1.9) |
となる。ここで、
となる。コンデンサーの容量を変化させて、図1.3 を描くことにより、式1.10を用いてQ値を求めることができる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成17年5月13日
![\includegraphics[keepaspectratio, scale=1.0]{figure/resonance/series_resonant.eps}](img27.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/resonance/resonance_curve.eps}](img28.png)
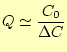
![\includegraphics[keepaspectratio, scale=1.0]{figure/resonance/capacitance_curve.eps}](img42.png)