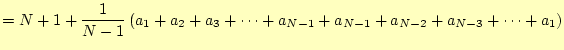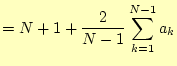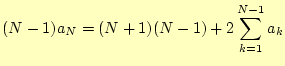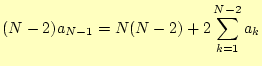5 付録
5.1 クイックソートの計算量
QuickSort()関数が最初に呼び出されたときの比較
lower<=upper&&data[lower]<=div
lower<=upper&&data[upper]>div
の実行回数
は、| (1) |
となる。もちろん、
となる。この漸化式から、
と変形しておく。つぎに、この式の
を利用する。式(3)から式(4)の辺々を差し引いて整理す ると、
| (5) |
となる。さらに、整理を進めると
| (6) |
となる。両辺を、
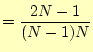 |
||
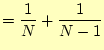 |
(7) |
となる。ここで、
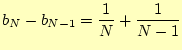 |
(8) |
となり、階差数列を用いて容易に計算できる。すなわち、
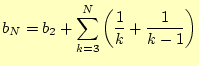 |
(9) |
である。
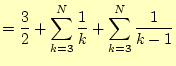 |
||
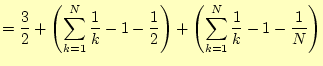 |
||
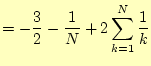 |
(10) |
となる。ここで、
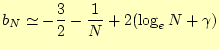 |
(11) |
となる。右辺の
| (12) |
となる。
| (13) |
となる。
![]() はsort[]の要素の比較回数を表す。したがって、
はsort[]の要素の比較回数を表す。したがって、![]() が大きい場合の比較回数は、
が大きい場合の比較回数は、
![]() となる。
となる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成17年10月27日