7 それぞれの方法の比較
7.1 解への収束速度
図8に、これまでに示した4つの方法の解への近 づき具合を示す。ニュートン法と割線法が収束が早いことが分る。先に示した 通り二次収束になっている。一方、二分法とはさみうち法は一次収束であるこ とがグラフより分かる。二分法は、10回の計算で、ニュートン法や割線法は収束が早く良さそうであるが、次に示すように解へ収束 しない場合があり問題を含んでいる。問題に応じて、計算方法を使い分けるべ きである。
7.2 ニュートン法の問題点
アルゴリズムから、2分法とはさみうち法は解に必ず収束する3。これらの 方法は、収束のスピードが遅いのが欠点である。一方、ニュートン法と割線法 は収束するとは限らない。初期条件に依存する場合がある。厳密にその条件を 求めるのは大変なので、初期条件により収束しない実例を示すことにする。非線形方程式
| (14) |
を計算することを考える。これは、初期値のより、収束しない場合がある。例 えば初期値
このようにニュートン法は解に収束しないで、振動する場合がある。こうなる と、プログラムは無限ループに入り、永遠に計算し続ける。これは資源の無駄 遣いなので、慎むべきである。通常は、反復回数の上限を決めて、それを防ぐ。 ニュートン法を使う場合は、この反復回数の上限は必須である。
ニュートン法で収束する必要条件が分かればこの問題は解決する。しかし、そ
れを探すのは大変である。というか私には分からない。一方、十分条件は簡単
にわかる。閉区間![]() で、
で、
![]() のような関数を考える。
このとき、
のような関数を考える。
このとき、
- 常に
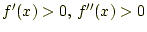 で、初期値が
で、初期値が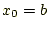 の場合
の場合
- 常に
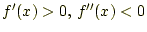 で、初期値が
で、初期値が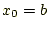 の場合
の場合
実際には収束しない場合のほうが稀であるので、ニュートン法は非常に強力な 非線型方程式の解法である。ただ、反復回数を忘れないことが重要である。ま た、二分法と組み合わせて使うことも考えられる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年9月10日
![\includegraphics[keepaspectratio, scale=0.7]{figure/Graph/speed_comv.eps}](img85.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/comv_hasan/hasan.eps}](img94.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/comv_hasan/comb.eps}](img95.png)