3 ガウス・ジョルダン法
逆行列が不要であれば、ガウス・ジョルダン法よりも、後で述べるLU分解の法 が計算速度は速い。しかし、教育的効果を考えると、両方の方法を知っておく のは良いことです。3.1 基本的な考え方
ガウス・ジョルダン(Gauss-Jordan)法というのは、連立方程式 (4)を次にように変形させて、解く方法である。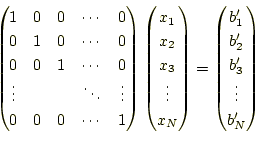 |
この式から明らかに、求める解
をガウス・ジョルダン法で解を求める。
まずは、1行目の![]() の係数を1に、2と3行目のそれは0にします。そのために、
1行目は
の係数を1に、2と3行目のそれは0にします。そのために、
1行目は![]() の係数の値で割る。2行目と3行目は、1行目に適当な係数を掛けて引く。次の
ようにする。
の係数の値で割る。2行目と3行目は、1行目に適当な係数を掛けて引く。次の
ようにする。
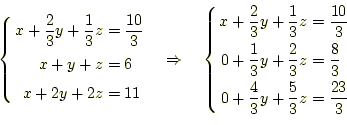 |
つぎに、2行目の
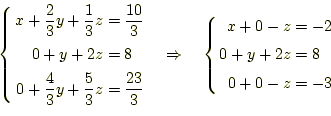 |
同じことを
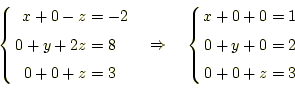 |
となる。従って、連立方程式(10)の解は、
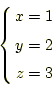 |
となる。これがガウス・ジョルダン法である。もっともらしい名前が付けられているが、 大したことなはい。
これで、ガウス・ジョルダン法が理解できたと思う。もう少し数学的に
その内容を説明する2。
そのために、次の線形行列方程式を考える。ここでは、紙面の関係で係数行
列が
![]() について述べるが、一般的に
について述べるが、一般的に![]() への拡張は容易である。
への拡張は容易である。
ここで、
| (16) | ||
| (17) |
が分かる。もちろん、
式(15)について、以下のことが容易に分かる。
-
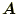 の任意の2行を入れ替えて、それに対応する
の任意の2行を入れ替えて、それに対応する
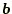 と
と
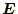 を入れ替えた場合、
を入れ替えた場合、
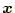 や
や
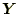 の値と順序は変わらない。た
だし、
の値と順序は変わらない。た
だし、
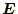 はもはや単位行列ではない。これは連立方程式の順序を入れ替
えて書いていることに相当している。
はもはや単位行列ではない。これは連立方程式の順序を入れ替
えて書いていることに相当している。
-
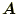 の任意の行を、その行と別の行との線形結合に置き換え、同
時に対応する
の任意の行を、その行と別の行との線形結合に置き換え、同
時に対応する
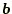 と
と
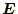 も同様に置き換える。この場合、
も同様に置き換える。この場合、
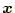 と
と
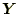 の値と順序は変わらない。当然、この場合も
の値と順序は変わらない。当然、この場合も
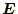 はもはや単
位行列ではない。
はもはや単
位行列ではない。
-
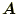 の任意の2列を入れ替えて、それに対応する
の任意の2列を入れ替えて、それに対応する
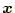 と
と
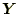 の行を入れ替えれば、
の行を入れ替えれば、
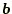 と
と
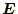 の順序は入れ替える必要
は無い。この場合、解の行の順序が変わるので、最後に元に戻す操作が必要
になる。
の順序は入れ替える必要
は無い。この場合、解の行の順序が変わるので、最後に元に戻す操作が必要
になる。
この3つの操作を組み合わせて、係数行列
![]() を単位行列に変換するのが
ガウス・ジョルダン法である。
を単位行列に変換するのが
ガウス・ジョルダン法である。
![]() が単位行列に変換されれば、右辺に
が単位行列に変換されれば、右辺に
![]() と
と
![]() が表れる。したがって、解と逆行列が求められたことに
なる。もし、逆行列が不要であれば
が表れる。したがって、解と逆行列が求められたことに
なる。もし、逆行列が不要であれば
![]() だけ計算し、逆行列のみ必要
であれば
だけ計算し、逆行列のみ必要
であれば
![]() のみ計算する。
のみ計算する。
3.2 ピボット選択
先に示した、ガウス・ジョルダン法の3つの基本操作のうち、2番目しか使わな い方法を「ピボット選択なしのガウス・ジョルダン法」と言う。最初、人 力で連立方程式を解いた方法である。この方法の明らかにまずい点は、もし1に したい対角要素がゼロの場合、計算ができなくなってしまうところにある。この割る要 素をピボット(pivot)と言う。ゼロでないにしても、そのピボットが非常 に小さい値の場合、丸め誤差が大きくなり問題である3。このようなことから、普通は ピボット選択なしのガウス・ジョルダン法というものは考えられない。この問題を避けるためにどうするかというと、ピボット選択という方法を使う。方法は簡 単で、先に示した3つの基本操作のうち、1番目と3番目を使って、対角に素性の良い要素 をもってくる。1番目の操作のみを用いて行を入れ替える方法を、部分ピボット選択 (partial pivoting)と言う。1番目の操作と3番目の操作を使って、行と列を入れ替え るのを完全ピボット選択(full pivoting)と言う。すでにある程度出来上がっている 単位行列を壊したくないので、ピボットの選択は操作している行の下の行から選ばなく てはならない。
部分ピボット選択の方が明らかに簡単である。解の行列を入れ替える必要が無い からである。その場合、行の入れ替えしかしないので、ピボットはその列から選 ばなくてはならない。完全ピボット選択の方が選べる要素が多いが、 最終的な解の精度はあまり変わらないようである。したがって、ここではプログ ラムの簡単な部分ピボット選択で計算する事にする。
次に考えなくてはならないのは、ピボットを選択する基準である。簡単に言えば、 大きな要素選択すれば大体よい。しかし、ある行を100万倍して、それに 対応する右辺の行も100万倍することもできるので、ただ大きいというだけ では問題がありそうである。どうするかと言うと、各方程式の最大係数を1に規 格化して、最大のものをピボットに選ぶことが行われている。この方法を陰 的ピボット選択(implicit pivoting)と呼ぶ。
これで、ピボットの問題も片付いたので、フローチャートを書いてみる。
3.3 フローチャート
ガウス・ジョルダン法のフローチャートを図1に示す。ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年11月9日
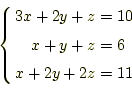

![\includegraphics[keepaspectratio, scale=0.8]{figure/flow_gj.eps}](img52.png)