1 常微分方程式
1.1 常微分方程式のイメージ
微分方程式は、物理や工学の分野で問題を解く強力なツールばかりか、生物や経済などで も広く応用されています。皆さんにぜひとも身に付けてもらいたいスキルです。微分方程 式を使うためには、方程式をる作ことと解くことが必要です。ここでは、微分方程式を解 くこと、特に数値計算により非常に精度の良い近似値を求める方法を学習します。微分方 程式では解析解が無いのが普通です。解析解は無いけれども、精度良く近似値を求めたい 状況にしばしば遭遇します。このような時、数値計算の出番です。数学に無い面白さがあ りますので、楽しんでください。すでに学習したように、独立変数が二つ以上の多変数の関数の微分(偏微分)を含む微分方 程式を偏微分方程式(partial differential equation)といいます。それに対して、一変 数の関数の微分を含む方程式を常微分方程式(ordinary differential equation)といいま す。ここでは、常微分方程式、特に1 階の場合の解の近似値を求める方法を学習します。 学習する方程式は
です。1階だといってバカにはできません。後で述べますが、これが数値計算できると、 どんな高階の常微分方程式も同じ方法で数値計算ができます。
ここでの主題は、この微分方程式を満たす![]() を求めることです。計算を進める前にこ
の方程式が何を表すか考えましょう。式(1) の左辺は、解
を求めることです。計算を進める前にこ
の方程式が何を表すか考えましょう。式(1) の左辺は、解![]() の導関数です。即ち、解の曲線の接線を表します。導関数の値が座標
の導関数です。即ち、解の曲線の接線を表します。導関数の値が座標![]() の関数になっ
ているわけです。座標
の関数になっ
ているわけです。座標![]() が決まれば、曲線の傾きが決まります。
が決まれば、曲線の傾きが決まります。
それでは、この常微分微分方程式のイメージをつかんでもらいましょう。それには、実際 の微分方程式を考えるのが良いでしょう。例えば、
を考えます。いかにも難しげな微分方程式ですが、これには解析解があります。解析解は とりあえずおいといて、この式の右辺を考えます。この式は接線の傾きを表すので、各座 標での傾きを書いてみましょう。この傾きを方向場と言います。すると図 1のようになります。この図から、大体の解の様子がわかりま す。
実際の解は、
| (3) |
です。1階の微分方程式ですから、1個の未知数を含みます。この未知数の値が異なる5本 の曲線と、先ほどの方向場を重ねて書き表してみます(図2)。微分方程 式の解である曲線
式(2)の微分方程式から、関数![]() の値を得るにはもう一つ条件が必
要です。通常この条件は、
の値を得るにはもう一つ条件が必
要です。通常この条件は、
![]() のように与えられます。これを初期値といい、初
期値が与えられるものを初期値問題といいます。一方、2 点以上のxで定めるyの値が決まっ
ているような問題を境界値問題といいます。ここでは、もっぱら初期値問題を解くことに
します。
のように与えられます。これを初期値といい、初
期値が与えられるものを初期値問題といいます。一方、2 点以上のxで定めるyの値が決まっ
ているような問題を境界値問題といいます。ここでは、もっぱら初期値問題を解くことに
します。
1.2 数値計算のイメージ
初期値問題を計算するルーチンの基礎的な考え方はどれも似通っており、次の通りです。 まず(1)式の微分方程式を、極限の| (4) |
のように変形できます。これを用いて、
この式と初期値
式(5)は、次の![]() 値は、もとの
値は、もとの![]() にそこでの傾き
にそこでの傾き
![]() に
に![]() の増分
の増分![]() を乗じたものを加えた形になっています。即ち、図
3の通りです。この図からも分かるようにこの方法をそのまま
適用した場合(オイラー法)、あまり精度がよくありません。出発点のみの導関数を用いて
いるため、終点付近では傾きが異なっています。刻み巾
を乗じたものを加えた形になっています。即ち、図
3の通りです。この図からも分かるようにこの方法をそのまま
適用した場合(オイラー法)、あまり精度がよくありません。出発点のみの導関数を用いて
いるため、終点付近では傾きが異なっています。刻み巾![]() を小さくすることによ
り解決は出来ますがその分、計算時間が必要になります。そのため、
を小さくすることによ
り解決は出来ますがその分、計算時間が必要になります。そのため、![]() と
と![]() の
間で、出来るだけ精度よく、この導関数を計算する工夫がいろいろ考えられています。以
降、その方法を示します。
の
間で、出来るだけ精度よく、この導関数を計算する工夫がいろいろ考えられています。以
降、その方法を示します。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年9月13日
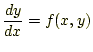
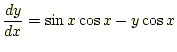
![\includegraphics[keepaspectratio, scale=1.0]{figure/direction_field.eps}](img13.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/solution.eps}](img15.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/sabun.eps}](img31.png)