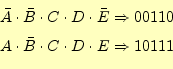クワイン法、あるいはクワイン・マクラスキー法はいろいろな表現の仕方があ
ります。ここでは、参考文献[1]に従いクワイン法とクワイン・
マクラスキー法を分けて説明します。最終的には、クワイン・マクラスキー法
を理解することを目指します。これを理解するために、直感的に分かりやすい
クワイン法から説明します。
実はカルノー図法も同じですが、クワイン・マクラスキー法はブール代数の次
の式を利用します。
カルノー図の場合、隣り合うセルは1ビットのみ異なるため、図を用いて2次元
的に一度にこの処理を行います。この処理は、コンピューター苦手で、さらに
変数が増えると大変になります。
クワイン・マクラスキー法は、手間はかかりますが、ひとつずつ式
(1)を利用して式を簡単化します。同じ手順を繰り返すこ
とにより、処理を行いますので、コンピューター向けと言えます。また、変数
が増えた場合、カルノー図よりも簡単になります。
ここは、主に参考文献[2]を参考にしました。そこでは、クワイ
ン・マクラスキー方と呼んでいますが、ここではクワイン法と呼ぶことにしま
す。呼び方なんてどうでもよいか、内容を理解することが重要です。
実際の例に従って、クワイン法により論理関数を簡単化する手順を示します。
以下の論理関数を簡単化することを考えます。
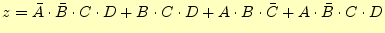 |
(2) |
まずはじめに、これを主加法標準展開します。すると、
となります。これから、式(1)を用いて冗長な項(他の項
の表現に含まれる項)を1つずつしらみつぶしに消します。
機械的にこの操作を行うために圧縮表というものを使います。それを図
1に示します。これにより、項を削減して論理関
数を簡単化しているのですが、その方法を以下に手順を追って説明します。
- 加法標準展開した各項(最小項)を左端に書きます。並べる順序は、各
項を2進数と見立て、小さい数から並べます。そのままの項は1、否定の
項はゼロをあらわすと考えます。例えば
です。
- 次に、式(1)を利用して、第1次の圧縮を行います。
この場合、可能な組み合わせすべてについて圧縮を行います。そのため、
最小項よりも第1次圧縮の方が項数が増えることがあります。圧縮でき
ない場合は、その最小項は四角で囲みます。図
![[*]](crossref.png) では圧縮できない最小項はありません。
では圧縮できない最小項はありません。
- 次に、同じように第2次圧縮を行います。2次圧縮以降では、同一の項
が現れるので注意が必要です。ここでも、圧縮できない項は四角で囲み
ます。図1では、
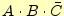 と
と
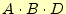 がそれにあたります。
がそれにあたります。
- 全ての項が圧縮できなくなるまで、同じことを繰り返します。
このようにして、圧縮表を完成させます。この圧縮できない項を主項と言いま
す。普通の人は、これで以下のように簡単化が完了したと錯覚します。
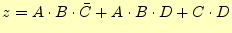 |
(4) |
しかし、これはまだ簡単化が可能です。この式は未だ冗長です。
さらに簡単化するためには、主項図を作成して冗長を調べます。表
1に主項図を示します。この図は、以下の手順で作
成します。
- 表の左端の列に、圧縮表で求めた主項を書きます。そして、上端の行
には最小項を書きます。この表により、主項と最小項の関係を調べます。
- 最小項を包含する主項に○印をつけます。この○印の数は、
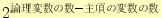 になることに注意
してください。さらに、各最小項は少なくとも1つは○印が付くことに
も注意しましょう。
になることに注意
してください。さらに、各最小項は少なくとも1つは○印が付くことに
も注意しましょう。
- それぞれの最小項のうち、○印が1つのものは◎印に変更します。この
◎印がついた主項は必須項になります。
- ◎印がついた主項を全て◎印に変更します。
これで、主項図は完成です。後は、これを利用して冗長な主項を見つけ、必要
なもののみで論理関数を構成することです。
表:
主項図。ここでは、表のカラムのサイズの都合上、乗法の記号
 を省略しています。
を省略しています。
| <#537#> |
最小項 |
| |
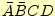 |
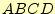 |
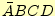 |
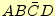 |
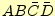 |
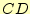 |
◎ |
◎ |
◎ |
|
|
◎ |
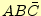 |
|
|
|
◎ |
◎ |
|
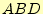 |
|
○ |
|
○ |
|
|
この主項図から、最も簡単化された論理関数を求めます。方法は簡単で、まず
必須項を書き出します。そして、残りの主項で最小項を全て含む最も簡単な組
み合わせを探します。もし、◎印が1つも含まれない最小項が有れば適当な主
項を選択すれば良いということです。
表1の場合、必須項のみで全ての最小項を含みます
ので、簡単化は
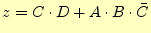 |
(5) |
となります。表1から明らかなように、
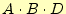 が冗長な項です。
クワイン・マクラスキー法は、クワイン法と非常によく似ています。ほとんど
同じと言っていいかもしれません。ただ、最初にクワイン・マクラスキー法を
説明すると、操作の内容が理解しにくいためにクワイン法を説明しました。実
際には、クワイン・マクラスキー法が重要なので、先に示したクワイン法は忘
れてもかまいません。
が冗長な項です。
クワイン・マクラスキー法は、クワイン法と非常によく似ています。ほとんど
同じと言っていいかもしれません。ただ、最初にクワイン・マクラスキー法を
説明すると、操作の内容が理解しにくいためにクワイン法を説明しました。実
際には、クワイン・マクラスキー法が重要なので、先に示したクワイン法は忘
れてもかまいません。
クワイン法とクワイン・マクラスキー法の違いは、圧縮表の作り方だけです。
主項図は同じです。クワイン法では論理変数を用いて圧縮表を作成しましたが、
クワイン・マクラスキー方では2進数を用います。2進数を10進数表示して、圧
縮する方法もあります [3]。10進数で圧縮表を作ると
表が小さくなって良いのですが、混乱する可能性が有りますので、ここでは2
進数で圧縮表を作成します。教科書と同じ方法です。
それでは、違う例題を用いて圧縮表の作り方を説明します。次の論理関数を簡
単化することを考えます。
クワイン・マクラスキー法の完成した圧縮表を図2に示
します。この圧縮表の作成方法は、クワイン法と似ていますが詳細は異なりま
す。以下にその手順を示します。
- まず、与えられた論理関数を主加法標準展開します。
- 最小項を2進数で表現します。そのままの変数は1、否定の
はゼロをあらわすと考えます。例えば
です。
- 加法標準展開した各項(最小項)を圧縮表の左端に書きます。最小項を
並べる場合、2進数に変換した1の数によりグループ分けします。そして、
グループの中で、数の小さい項から上から順に並べます。
- 次に、式(1)を利用して、第1次の圧縮を行います。
この場合、可能な組み合わせすべてについて圧縮を行います。そのため、
最小項よりも第1次圧縮の方が項数が増えることがあります。圧縮でき
ない場合は、その最小項は四角で囲みます。図2
では
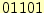 がそれにあたります。この四角で囲まれたものが主項にな
ります。
がそれにあたります。この四角で囲まれたものが主項にな
ります。
- 次に、同じように第2次圧縮を行います。2次圧縮以降では、同一の項
が現れるので注意が必要です。ここでも、圧縮できない項は四角で囲み
ます。
- 全ての項が圧縮できなくなるまで、同じことを繰り返します。
以上の操作により圧縮表が完成します。後は完成した図![[*]](crossref.png) の圧縮表から、主項図を作成します。主項図の作成要領は、クワイン法と
同じなのでここでは説明しません。
の圧縮表から、主項図を作成します。主項図の作成要領は、クワイン法と
同じなのでここでは説明しません。
表2に完成した主項図を示します。この主項図から、簡
単化された論理関数は、
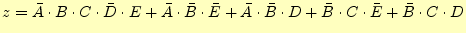 |
(6) |
となります。
表 2:
主項図。ここでは、表のカラムのサイズの都合上、2進数で表示し
ています。もちろん、論理変数で表示しても問題ありません。
| <#582#> |
最小項 |
| |
00000 |
00010 |
00100 |
00011 |
00110 |
10100 |
00111 |
01101 |
10110 |
| 01101 |
|
|
|
|
|
|
|
◎ |
|
|
| 00__0 |
◎ |
◎ |
◎ |
|
◎ |
|
|
|
|
|
| 00_1_ |
|
◎ |
|
◎ |
◎ |
|
◎ |
|
|
|
| _01_0 |
|
|
◎ |
|
◎ |
◎ |
|
|
◎ |
|
| _011_ |
|
|
|
|
◎ |
|
◎ |
|
◎ |
◎ |
クワイン・マクラスキー法を用いて、論理関数を簡単化する手順をまとめてお
きます。これは大きく分けて、3つの部分から成り立っています。圧縮表と主
項図、そして論理関数の作成です。それぞれについて、その手順をまとめます。
まず、圧縮表の作成手順は以下の通りです。
- まず、与えられた論理関数を主加法標準展開します。
- 最小項を2進数で表現します。そのままの変数は1、否定の
はゼロをあらわすと考えます。例えば
です。
- 加法標準展開した各項(最小項)を圧縮表の左端に書きます。最小項を
並べる場合、2進数に変換した1の数によりグループ分けします。そして、
グループの中で、数の小さい項から上から順に並べます。
- 次に、
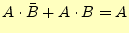 を利用して、第1次の圧縮を行います。
この場合、可能な組み合わせすべてについて圧縮を行います。そのため、
最小項よりも第1次圧縮の方が項数が増えることがあります。圧縮でき
ない場合は、その最小項は四角で囲みます。この圧縮できない項を主項
と言います。
を利用して、第1次の圧縮を行います。
この場合、可能な組み合わせすべてについて圧縮を行います。そのため、
最小項よりも第1次圧縮の方が項数が増えることがあります。圧縮でき
ない場合は、その最小項は四角で囲みます。この圧縮できない項を主項
と言います。
- 次に、同じように第2次圧縮を行います。2次圧縮以降では、同一の項
が現れるので注意が必要です。ここでも、圧縮できない項は四角で囲み
ます。
- 全ての項が圧縮できなくなるまで、同じことを繰り返します。
次にこの圧縮表を用いて主項図を作成します。その手順は、以下の通りです。
- 表の左端の列に、圧縮表で求めた主項を書きます。そして、上端の行
には最小項を書きます。この表により、主項と最小項の関係を調べます。
- 最小項を包含する主項に○印をつけます。この○印の数は、
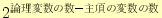 になることに注意
してください。さらに、各最小項は少なくとも1つは○印が付くことに
も注意しましょう。
になることに注意
してください。さらに、各最小項は少なくとも1つは○印が付くことに
も注意しましょう。
- それぞれの最小項のうち、○印が1つのものは◎印に変更します。この
◎印がついた主項は必須項になります。
- ◎印がついた主項を全て◎印に変更します。
これで圧縮表は完成します。最後にこの圧縮表を用いて、簡単化された論理関
数を求めます。要領は以下の通りです。
- 必須項の和で論理関数を作ります。
- もし、◎印が1つも含まれない最小項が有れば、最も簡単な主項を選
択し、先の論理関数に加算します。
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年8月20日
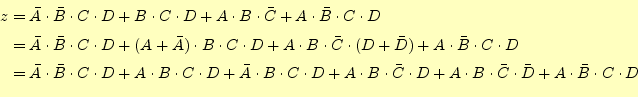
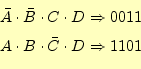
![[*]](crossref.png) では圧縮できない最小項はありません。
では圧縮できない最小項はありません。
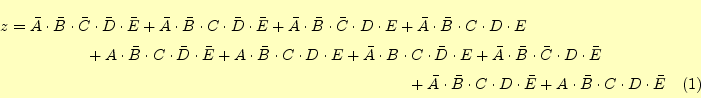
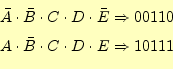
![[*]](crossref.png) の圧縮表から、主項図を作成します。主項図の作成要領は、クワイン法と
同じなのでここでは説明しません。
の圧縮表から、主項図を作成します。主項図の作成要領は、クワイン法と
同じなのでここでは説明しません。