[Previous: 1 はじめに] [Up: 座標系と微分演算子] [Next: 3 座標系の変換]
ベクトル量は座標系に依存しない。これは、ある場所の電場を考えると、その位置を直交
座標![]() で表そうが、極座標
で表そうが、極座標
![]() で表そうが、電場
で表そうが、電場
![]() は同じで
あることを言っている。次の通りである。
は同じで
あることを言っている。次の通りである。
| (1) |
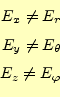 |
ベクトルは、座標系の取り方によらない幾何学上の物体として取り扱われることに注意し よう。実際これまでの所では、どんな座標系も用いていない。座標系の取り方に依存し ないという、と上手に表現している。
このことをもう少しわかりやすく2次元座標系で示す。図
1のように、ベクトル
![]() は座標系に全
く依存しない量である。位置が決まれば、その量は決まる。そして、その成分は直交座標
と極座標では、異なる。もちょっと、感のいい人は、それぞれの座標系の成分の関係は、
座標系の回転と同じであることがわかるであろう。ベクトル量の成分の変換は、回転の座
標変換と全く同じである。このことは、ベクトルの定義として、しばしば使われる。ここ
では、これ以上、深入りはしないこととするが、座標系によるベクトルの成分の変換は、座
標回転の変換と同じであることを以降の議論に用いる。ただし、これは直交座標系の間
の変換に限る。斜交座標系については、ここでは取り扱わない。
は座標系に全
く依存しない量である。位置が決まれば、その量は決まる。そして、その成分は直交座標
と極座標では、異なる。もちょっと、感のいい人は、それぞれの座標系の成分の関係は、
座標系の回転と同じであることがわかるであろう。ベクトル量の成分の変換は、回転の座
標変換と全く同じである。このことは、ベクトルの定義として、しばしば使われる。ここ
では、これ以上、深入りはしないこととするが、座標系によるベクトルの成分の変換は、座
標回転の変換と同じであることを以降の議論に用いる。ただし、これは直交座標系の間
の変換に限る。斜交座標系については、ここでは取り扱わない。