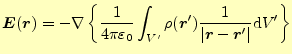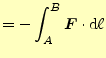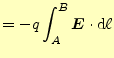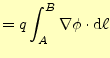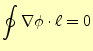実際に電場を計算するためのもう少し便利な式を導いておこう.静電場をあらわす一般化
されたクーロンの法則の式(
10)は
と書いてもよい.体積分の積分変数は
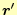
で,勾配

の微分の変数
は
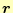
と異なるから,微分と積分を入れ替えることができる.ここで,右辺にある体
積積分を
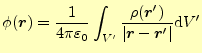 |
(20) |
とする.これは,全ての空間--宇宙全体--にわたっての積分である.この積分の値
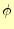
をスカラーポテンシャルと言う.このスカラーポテンシャルを導入することにより,
電場は,
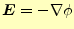 |
(21) |
と簡単に計算できる.以前,任意のベクトル場は管状と渦無しの場に分解できると述べた.
この式から,静電場は渦無しのベクトル場で,管状の部分が無いことが分かる.
次にスカラーポテンシャルの性質を調べる.電荷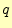 を静電場の中に置くと,
を静電場の中に置くと,
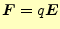 と
いう力を受ける.その力に抗して,その電荷を
と
いう力を受ける.その力に抗して,その電荷を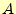 点から
点から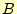 点まで,移動させるのに必要
な仕事
点まで,移動させるのに必要
な仕事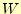 は
は
となる.以前,勾配

の積分のところで説明したように,この積分は経路に依存
しない.積分の両端の場所のみによって,この仕事量
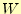
は決まるのである.仕事量
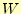
は,
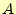
点に比べたときの
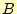
点での電荷
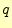
が持つエネルギーの増加をあらわしている.
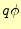
を位置によるエネルギー,すなわちポテンシャルエネルギーと解釈することがで
きる.よく考えると,この
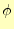
は電圧の定義とも等しい.ポテンシャル
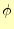
と言っ
ているが,これは電圧と言い替えても差し支えない.
式(18)から,電場の周回積分はゼロと分かっている.従って,
となる.これは,微小区間での電位差
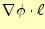
を足しあわせて,任意の閉
じた経路を積分するとゼロになると言っている.これは,回路で使うキルヒホッフの法則
の片割れである.式(
23)は静電場で適用され,キルヒホッフの法則は
交流のように時間的に変化する回路でも成立する--と言う反論がある.通常の回路の大
きさは,その動作周波数の波長に比べて,十分小さい.そのため,電磁気学的に見ると,
ほとんど静電場で近似できる.したがって,波長よりも十分小さい普通の回路では,式
(
23)は良い近似となる.一方,波長が短くなり,回路と同程度の大きさに
なると,もはやキルヒホッフの法則は成り立たなくなる.
ホームページ:
Yamamoto's laboratory著者:
山本昌志
Yamamoto Masashi
平成19年7月12日
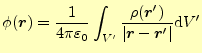
![]() を静電場の中に置くと,
を静電場の中に置くと,
![]() と
いう力を受ける.その力に抗して,その電荷を
と
いう力を受ける.その力に抗して,その電荷を![]() 点から
点から![]() 点まで,移動させるのに必要
な仕事
点まで,移動させるのに必要
な仕事![]() は
は