ガウス消去法とガウス・ジョルダン法は単純で,諸君が今まで連立1次方程
式を計算してきた方法と同じである.
ガウス消去法というのは,連立方程式
(4)を次にように変形させて,解く方法である.
このように式を変形する方法をガウスの消去法と言う.実際の変形方法については,次の
ガウス・ジョルダン法とほとんど同じでなので,次節を参考にすること.このように式が
変形できると後は簡単で,次にように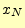 から
から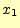 まで順次計算する.
まで順次計算する.
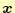 の値は,
の値は,
と求めることができる.この式は,
![$\displaystyle x_i=\frac{1}{a_{ii}^\prime}\left[ b_i^\prime-\sum_{j=i+1}^N a_{ij}^\prime x_j \right]$](img42.png) |
(8) |
とまとめることができる.これを使って,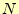 〜0まで処理することを後退代入と言う.
重要なことは,後ろ
〜0まで処理することを後退代入と言う.
重要なことは,後ろ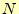 から処理することで,決して,
から処理することで,決して,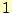 から処理することはできない.
ガウス消去法と後退代入により連立1次方程式は,コンピューターで容易に解くことがで
きる.
から処理することはできない.
ガウス消去法と後退代入により連立1次方程式は,コンピューターで容易に解くことがで
きる.
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年10月25日
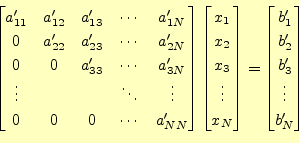
![]() から
から![]() まで順次計算する.
まで順次計算する.
![]() の値は,
の値は,
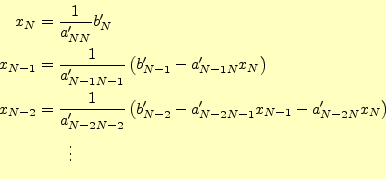
![$\displaystyle x_i=\frac{1}{a_{ii}^\prime}\left[ b_i^\prime-\sum_{j=i+1}^N a_{ij}^\prime x_j \right]$](img42.png)