1 波動方程式とは

ラプラス方程式が済んだので，次に波動方程式に移ろう．その前に，2階の偏微分方程式 の種類について説明しておく．2階の偏微分方程式は，ラプラス方程式のように楕円型， 次に学習する波動方程式のような双曲型，学習はしないが拡散方程式のような放物型に分 けられる．これが，2階の偏微分方程式の代表的な型である．これらの解法を知っておけ ば，自然現象の多くの問題を計算することができる．いうなれば，超基本の方程式である．

波動方程式は，名前が表しているように波の方程式である．自然科学では，波を扱うこと が非常に多い．光，電磁波，量子力学等の問題は全て波を取り扱っている．いろいろな場 面で出くわす波の方程式は簡単で，

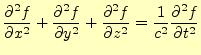$$\frac{\partial^2 f}{\partial x^2}+ \frac{\partial^2 f}{\partial y... ...rac{\partial^2 f}{\partial z^2}= \frac{1}{c^2}\frac{\partial^2 f}{\partial t^2}$$ (1)

と書き表すことができる．$c$は波の速度である．これは，3次元の場合で，時間を入れる と4次元の方程式になり，ちょっと計算するには複雑である．そこで，ここでは空間1次元， 時間1次元の2次元の方程式

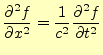$$\frac{\partial^2 f}{\partial x^2}= \frac{1}{c^2}\frac{\partial^2 f}{\partial t^2}$$ (2)

を数値計算で解くことを考える．

皆さんは，フーリエ級数を学習したときに，この方程式を解いたとはずである．ここでは， 数値計算により近似解を得る方法を学習する．もちろん，フーリエ級数で解いた解は，解 析解で完璧である．ただ，フーリエ級数が適用できるのは，空間が1次元の場合である．2 次元以上になると境界条件が簡単な場合に限り，フーリエ級数を用いて計算できる．境界 が複雑になると，数値計算で近似解を求めることが重要になる．数値計算は，空間が2次 元以上の問題で威力を発揮することになるが，ここでは学習のため，空間が1次元の問題 を解くことにする．

具体的な問題を例にして，学習を進める．比較的単純な問題として，図1の ような弦の振動を考える．これは，ギターのように両端が固定された弦である．ある時刻 $t$の位置$x$の変位を$u(x,t)$としている．この変位は波動方程式，

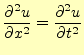$$\frac{\partial^2 u}{\partial x^2}= \frac{\partial^2 u}{\partial t^2}$$ (3)

を満たす．ただし，波の速度は$c=1$とした．こうしても，波動方程式を解くと言う意味 はそうは変わらないし，計算が楽になるメリットはある．

図 1: 時刻tの弦の様子．

ホームページ: Yamamoto's laboratory
著者: 山本昌志