7 波動方程式

`[`問1]
自由空間中のマクスウェルの方程式を示せ。

自由空間では、電流や電荷はない。したがって、マクスウェルの方程式の中で、 $\rho=0$ 、 $\boldsymbol{j}=0$ とすればよい。すると、自由空間での電磁場を表すマクスウェルの方程式

	$\displaystyle \div{\boldsymbol{E}}=0$
	$\displaystyle \div{\boldsymbol{B}}=0$
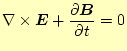	$\displaystyle \nabla\times \boldsymbol{E}+ \if 11 \frac{\partial \boldsymbol{B}}{\partial t} \else \frac{\partial^{1} \boldsymbol{B}}{\partial t^{1}}\fi =0$
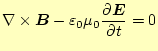	$\displaystyle \nabla\times \boldsymbol{B}-\varepsilon_0\mu_0 \if 11 \frac{\part... ...{E}}{\partial t} \else \frac{\partial^{1} \boldsymbol{E}}{\partial t^{1}}\fi =0$

が得られる。

[問2]
自由空間中のマクスウェルの方程式から、以下の波動方程式を導け。

$\displaystyle \nabla^2\boldsymbol{E}-\varepsilon_0\mu_0 \if 12 \frac{\partial \... ...{E}}{\partial t} \else \frac{\partial^{2} \boldsymbol{E}}{\partial t^{2}}\fi =0$

$\displaystyle \nabla^2\boldsymbol{B}-\varepsilon_0\mu_0 \if 12 \frac{\partial \... ...{B}}{\partial t} \else \frac{\partial^{2} \boldsymbol{B}}{\partial t^{2}}\fi =0$

自由空間では、電流や電荷はない。したがって、マクスウェルの方程式は

	$\displaystyle \div{\boldsymbol{E}}=0$
	$\displaystyle \div{\boldsymbol{B}}=0$
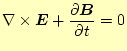	$\displaystyle \nabla\times \boldsymbol{E}+ \if 11 \frac{\partial \boldsymbol{B}}{\partial t} \else \frac{\partial^{1} \boldsymbol{B}}{\partial t^{1}}\fi =0$
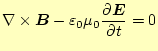	$\displaystyle \nabla\times \boldsymbol{B}-\varepsilon_0\mu_0 \if 11 \frac{\part... ...{E}}{\partial t} \else \frac{\partial^{1} \boldsymbol{E}}{\partial t^{1}}\fi =0$

となる。

この式のうち3番目のものの両辺に回転の演算子を作用させると、

0	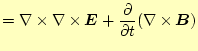$\displaystyle =\nabla\times \nabla\times \boldsymbol{E}+ \if 11 \frac{\partial ... ... t} \else \frac{\partial^{1} }{\partial t^{1}}\fi (\nabla\times \boldsymbol{B})$
	マクスウェルの方程式の4番目の式)より
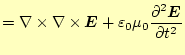	$\displaystyle =\nabla\times \nabla\times \boldsymbol{E}+\varepsilon_0\mu_0 \if ... ...bol{E}}{\partial t} \else \frac{\partial^{2} \boldsymbol{E}}{\partial t^{2}}\fi$	(39)

となり、電場のみの式にできる。ここで、右辺第一項であるが、これはベクトル恒等式 $\nabla\times \nabla\times \boldsymbol{A}=\nabla (\div{\boldsymbol{A}})-\nabla^2\boldsymbol{A}$ を使い、

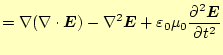0	$\displaystyle =\nabla (\div{\boldsymbol{E}})-\nabla^2\boldsymbol{E} +\varepsilo... ...bol{E}}{\partial t} \else \frac{\partial^{2} \boldsymbol{E}}{\partial t^{2}}\fi$
	マクスウェルの方程式の1番目の式より
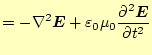	$\displaystyle =-\nabla^2\boldsymbol{E}+\varepsilon_0\mu_0 \if 12 \frac{\partial... ...bol{E}}{\partial t} \else \frac{\partial^{2} \boldsymbol{E}}{\partial t^{2}}\fi$

と変形できる。これで、電場のみの式となった。

同様のことを磁場について行う。マクスウェルの方程式の4番目の式の両辺の回転の演算子を作用させると

0	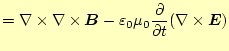$\displaystyle =\nabla\times \nabla\times \boldsymbol{B}-\varepsilon_0\mu_0 \if ... ... t} \else \frac{\partial^{1} }{\partial t^{1}}\fi (\nabla\times \boldsymbol{E})$
	$\displaystyle \qquad\qquad\nabla\times \nabla\times \boldsymbol{A}=\nabla (\div{\boldsymbol{A}})-\nabla^2\boldsymbol{A}$ とマクスウェルの方程式の3番目の式より
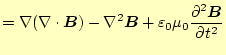	$\displaystyle =\nabla (\div{\boldsymbol{B}})-\nabla^2\boldsymbol{B} +\varepsilo... ...bol{B}}{\partial t} \else \frac{\partial^{2} \boldsymbol{B}}{\partial t^{2}}\fi$
	マクスウェルの方程式の2番目の式より
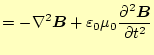	$\displaystyle =-\nabla^2\boldsymbol{B}+\varepsilon_0\mu_0 \if 12 \frac{\partial... ...bol{B}}{\partial t} \else \frac{\partial^{2} \boldsymbol{B}}{\partial t^{2}}\fi$

が得られる。

以上の操作により得られた電場と磁場の式を整理すると、

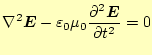$\displaystyle \nabla^2\boldsymbol{E}-\varepsilon_0\mu_0 \if 12 \frac{\partial \... ...{E}}{\partial t} \else \frac{\partial^{2} \boldsymbol{E}}{\partial t^{2}}\fi =0$
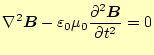$\displaystyle \nabla^2\boldsymbol{B}-\varepsilon_0\mu_0 \if 12 \frac{\partial \... ...{B}}{\partial t} \else \frac{\partial^{2} \boldsymbol{B}}{\partial t^{2}}\fi =0$

が得られる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志

Yamamoto Masashi
2005-11-15