3 静磁場

[問1]

半径$a$ の無限に長い円柱状の導体内を、一様な密度で強さ$I$ の電流が流れているとき、 円柱の内外に生じる磁束密度を求めよ。

軸対称問題なので，円柱座標系を使うのが簡単である．電流があるときの静磁場は，アン ペールの法則

$$\nabla\times \boldsymbol{B}=\mu_0\boldsymbol{j}$$

を用いると簡単に計算できる．円柱状の導体内部の電流密度 $\boldsymbol{j}$ は，$I/\pi a^2$ で ある．当然，導体外部では $\boldsymbol{j}=0$ となる．

アンペールの法則をストークスの定理を用いて，積分形に書き改めると，

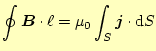$$\oint \boldsymbol{B}\cdot\ell=\mu_0\int_S\boldsymbol{j}\cdot\mathrm{d}S$$ (35)

となる．円柱の中心を$r=0$ として，円柱の内部と外部でこれを積分することを考える． 当然，磁場は円柱座標系のr方向成分$B_r$ のみである．従って，積分は，

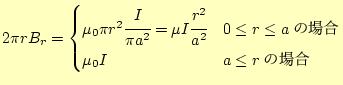$$2\pi rB_r= \begin{cases}\mu_0\pi r^2\cfrac{I}{\pi a^2}=\mu I\cfra... ...a^2} & 0\leq r\leq a\text{の場合} \mu_0 I & a \leq r\text{の場合} \end{cases}$$ (36)

となる．これから，磁束密度は，

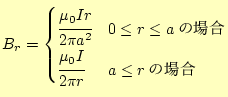$$B_r= \begin{cases}\cfrac{\mu_0 I r}{2\pi a^2} & 0\leq r\leq a\text{の場合} \cfrac{\mu_0 I}{2\pi r} & a \leq r\text{の場合} \end{cases}$$ (37)

と求められる．

[問2]

図の直線電流$I$ のABの部分が、図のP点につくる磁束密度は

$$B(P)=\frac{\mu_0I}{4\pi R}\left[\cos\theta_1-\cos\theta_2\right]$$

で与えられることを示せ。

点Oから直線電流に沿った座標を$x$ とする．Aの方向が負でBの方向が正とする．このとき の微小磁場は，ビオ・サバールの法則より

$$\mathrm{d}\boldsymbol{B}=\frac{\mu_0 I}{4\pi r^2}\frac{\mathrm{d}x\times\boldsymbol{r}}{r}$$

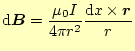となる．ここで，P点での磁場は紙面と垂直方向であり， $\vert\mathrm{d} x\times\boldsymbol{r}/r\vert=\sin\theta \mathrm{d}x$ となる．xの位置によらず磁場の方向は同じなの で， $\mathrm{d}B$ とスカラーで書いても良いだろう．微小磁場は，

$$\mathrm{d}B=\frac{\mu_0 I\sin\theta\mathrm{d}x}{4\pi r^2}$$

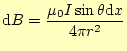となる．これを積分すればよいのだが，そのために，

$$\tan\theta=-\frac{R}{x} r\sin\theta=R$$

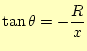をつかう．これらから，

$$\mathrm{d}x=\frac{R}{\sin^2\theta}\mathrm{d}\theta r=\frac{R}{\sin\theta}$$

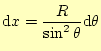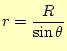これらを使うと，

$$\mathrm{d}B=\frac{\mu_0I}{4\pi R}\sin\theta\mathrm{d}\theta$$

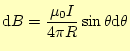となり，AからBまで積分を行うと，

$$B =\int_{\theta_1}^{\theta_2}\frac{\mu_0I}{4\pi R}\sin\theta\mathrm{d}\theta$$

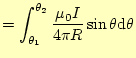$$=\frac{\mu_0I}{4\pi R}\left[\cos\theta_1-\cos\theta_2\right]$$

となる．

ホームページ: Yamamoto's laboratory
著者: 山本昌志