4 マクスウェルの方程式
ここでは、静電場を記述する式から出発し、電荷保存則とFaradayの電磁誘導の法則が成 り立つように、電磁場の発散と回転の式を拡張した。これにより、電磁場(| (35) | ||
| (36) | ||
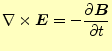 |
(37) | |
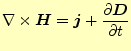 |
(38) |
となる。ただし、電磁場がある媒質の性質を決める誘電率
| (39) | ||
| (40) |
の関係がある。
もう一度言うが、全ての変数は位置
![]() と時間
と時間![]() の関数となっている。これが電磁
場を記述する完全な方程式である。これが計算できれば全ての電磁気の問題は解けること
になる。
の関数となっている。これが電磁
場を記述する完全な方程式である。これが計算できれば全ての電磁気の問題は解けること
になる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月24日