3 静電場のエネルギー

原理的には、クーロンの法則が静電気学の全てである。過不足なく、この法則 だけで、静電気に関するすべての物理的な現象が説明できる。この法則は、力 と電荷の関係を述べているにすぎない。ここで新しい概念、エネルギーと言う ものを導入する。これは、力学におけるニュートンの運動の法則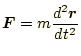

$$\boldsymbol{F}=m\frac{d^2\boldsymbol{r}}{dt^2}$$ (12)

に加えて、エネルギーの概念を導入することと似ている。古典力学の現象は全 て、ニュートンの運動の法則から説明できるが、エネルギーの概念を導入する ことで、問題の洞察力を飛躍的に増大できる。エネルギーの概念を全く使わな いで、古典力学の問題を解くような人はいないであろう。同じように、静電場 にもエネルギーの概念を導入する。

まずはじめに、無限に離れた2つの電荷$Q_1Q_2$を、距離$r$の間隔になるよう に配置する場合の仕事$W$を考える。この系にする仕事は、 $W=$力$\times$距離である。したがって、電荷$Q_1$を固定して、$Q_2$を無限 遠点から、距離$r_0$まで近づけるために、外部の何かがする仕事は、

$$\begin{aligned}W &=\int_{-\infty}^{r_0}\boldsymbol{F}(\boldsymb... ...silon r^2}dr\ &=\frac{Q_1Q_2}{4\pi\varepsilon r_0} \end{aligned}$$

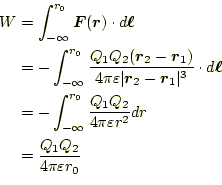である。外部の何かが、この電荷の配置を作るために、これだけの仕事をした のである。すると、この2つの電荷の分布は、その仕事の分だけエネルギーを 蓄えるはずである。これは、力学の問題のばねの問題とそっくりである。ばね の場合は、それが押し縮められたとき、ばねにエネルギーが蓄えられた。この 問題も、両方の電荷の間に仮想的なばねがあり、それが押し縮められたと考え ても良いのだろうか?。そのように考えても、差し支えは無い。ただ、ここで はもうちょっと便利な方法を考える。以前、話したように場の考え方に立つこ とにする。この方が、将来複雑な問題を解く場合、圧倒的に有効である。

静電場のエネルギーを教科書の方法で説明する。これは、コンデンサーを用い た説明である。電極の面積$S$で間隔$L$のコンデンサーを考える。この場合、 電極の一辺の長さは、電極間に比べて、十分大きいとする。これの両端に、 $-Q$と$+Q$の電荷があるような状況について、計算する。この場合、コンデン サーの中の電場 $\boldsymbol{E}$は、ガウスの法則の微分形

$$\nabla\cdot\boldsymbol{E}=\frac{\rho}{\varepsilon}$$ (14)

より²、両辺を積分すると、

$$\begin{aligned}\int\nabla\cdot\boldsymbol{E}dV&=\int\frac{\rho}... ...ol{E}\cdot\boldsymbol{n}ds&=\frac{Q}{\varepsilon}\ \end{aligned}$$

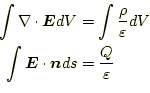となる。コンデンサー内部の電場は、ほぼ一様なので、

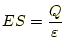$$ES=\frac{Q}{\varepsilon}$$ (16)

となる。驚いたことに、コンデンサー内部の電場の大きさは、電極間距離$L$ に無関係なのである。コンデンサーの外側では、電場がゼロであることにも留 意して欲しい。

次に、このコンデンサーの負極から、正電荷$+\delta Q$だけ、正極に移動さ せた場合を考える。当然この$+\delta Q$は微小量で、電場の大きさの変化は 小さいとする。この場合、外部の何かが

$$W=EL\delta Q$$ (17)

の仕事をする必要がある。そうすると、コンデンサーの内部では

$$\begin{aligned}\delta U &= EL\delta Q\ &= \frac{Q}{\varepsilon_0 S}L\delta Q \end{aligned}$$

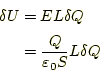のエネルギーが増えたはずである。したがって、もともと、電荷が無い状態か ら、両方の電極に$+Q$と$-Q$の電荷が蓄えられた状態になると、そこに蓄積さ れているエネルギー$U$は、

$$\begin{aligned}U&=\int_0^Q \frac{Q}{\varepsilon_0 S}LdQ\ &=\fr... ...psilon}{2}\int_V\boldsymbol{E}\cdot\boldsymbol{E}dv \end{aligned}$$

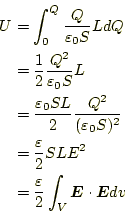となる。これは、密度 $\frac{\varepsilon_0}{2}\boldsymbol{E}\cdot\boldsymbol{E}$でエネル ギーが存在すると解釈する。

最後の方はかなり、論理が飛躍しているが、結果は正しい。重要なことは、静 電場のエネルギー密度は

$$=\frac{\varepsilon_0}{2}\boldsymbol{E}\cdot\boldsymbol{E}$$ (20)

である。

• 式(20)がエネルギー密度の次元になっている ことを確かめよ。
• このエネルギーの式から、コンデンサーの重要な関係式 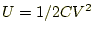$U=1/2 CV^2$ を求めよ

ホームページ: Yamamoto's laboratory
著者: 山本昌志