2 標準展開と反転ゲート

NORとNANDゲートのことを反転ゲートという。標準展開と反転ゲートは密接な 関わりがある。それを教科書の例をもって説明する。教科書の例は、

$$f=\bar{A}\cdot\bar{B}\cdot\bar{C} +\bar{A}\cdot B \cdot\bar{C} +\bar{A}\cdot B \cdot C +A \cdot B \cdot C$$ (1)

である。この論理式の真理値表は、表1の通りである。 元の式が論理和(OR)で各項がくくられているので、論理式の値が1になる組み 合わせが一目で分かる。

表 1: 問題の真理値表

$A$	$B$	$C$	$f$
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	1

この真理値表から、加法標準展開と乗法標準展開を計算する。後で分かること であるが、こうするとNANDやNORで表現するのが簡単になる。加法標準展開と 乗法標準展開は、カルノー図を使うのが簡単である。加法標準展開の場合、カ ルノー図は1に着目するのが良い。一方、乗法標準展開の場合は、0に着目する べきである。それぞれのカルノー図を図1と2に示す。

図 1: 1に着目したカルノー図

図 2: 0に着目したカルノー図

これから、式(1)は、それぞれ

$$f=\bar{A}\cdot\bar{C}+B \cdot C$$ 加法標準展開 (2)

$$f=(\bar{A}+C)\cdot(B+\bar{C})$$ 加法標準展開 (3)

となる。

これから、NANDゲートオンリーの式とNORゲートオンリーの式を導く。まずは じめに、NANDゲートオンリーは、加法標準形を使う。これを、以下のように変 形する。

$$\begin{aligned}f&=\bar{\bar{f}}\\ &=\overline{\overline{\bar{A}... ...line{\bar{A}\cdot\bar{C}}\cdot\overline{B \cdot C}} \end{aligned}$$

これで、すべての項が $\overline{x \cdot y}$の形になっているので、NANDゲー トオンリーである。

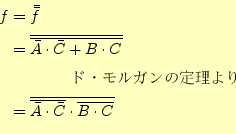同じことを、乗法標準形に施す。

$$\begin{aligned}f&=\bar{\bar{f}}\\ &=\overline{\overline{(\bar{A... ...line{\overline{(\bar{A}+C)}+\overline{(B+\bar{C})}} \end{aligned}$$

これは、すべての項が $\overline{x+y}$の形になっているので、NORゲー トオンリーである。

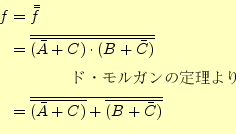これから分かるように、加法標準形や乗法標準形にすれば、NANDやNORオンリー の論理式に変形するのは簡単である。この変形をここでは、カルノー図を使っ て行ったが、もちろん他の方法でも良い。問題に合わせて、簡単な方法で標準 展開すればよいのである。

ホームページ: Yamamoto's laboratory
著者: 山本昌志