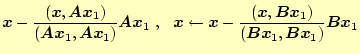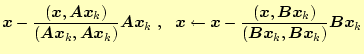前章の方法では最小の固有値しか求められないが,少し工夫するといくつかの固
有値を求められるようになる.
これには,実対称一般化固有値問題の特性を利用する.
すなわち,固有値問題の固有ベクトル
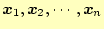 において,
において,
という性質である.つまり,固有ベクトルは行列
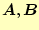 をはさんで直
交していると言える.
従って,いくつか小さい順から固有値が分かっていれば,それらと直交するベク
トルをさがすことで次の固有値が得られる.
をはさんで直
交していると言える.
従って,いくつか小さい順から固有値が分かっていれば,それらと直交するベク
トルをさがすことで次の固有値が得られる.
ベクトル
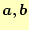 の直交化は次の式で与えられる.
の直交化は次の式で与えられる.
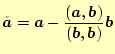 |
(10) |
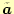 が
が
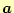 から
から
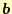 の成分を抜き出したものである.
このように,必要ない成分を抜き出すことができる.
の成分を抜き出したものである.
このように,必要ない成分を抜き出すことができる.
いま,すでに小さい方から固有値がいくつか求められていて,その固有ベクトル
が
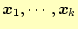 だとする.
ここから,次に小さい固有値を求めようとする.この求めるべき固有ベクトルは,
だとする.
ここから,次に小さい固有値を求めようとする.この求めるべき固有ベクトルは,
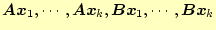 と直交していることが分かる.従って,これらの成分を抜き出しながら共役勾配
法で固有値を求めていけばよい.
と直交していることが分かる.従って,これらの成分を抜き出しながら共役勾配
法で固有値を求めていけばよい.
その手順を以下に示す.
-
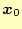 をランダム関数などを使い,適当に決める.
をランダム関数などを使い,適当に決める.
-
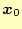 を直交化
を直交化
-
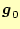 をもとめ,それを直交化
をもとめ,それを直交化
-
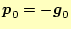 とする.
とする.
-
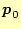 を直交化
を直交化
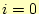
-
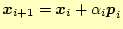
-
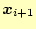 を直交化
を直交化
-
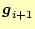 をもとめ,それを直交化
をもとめ,それを直交化
-
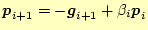
-
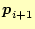 を直交化
を直交化
- 収束判定をして,収束が十分でなければ
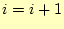 として,7に戻る.
として,7に戻る.
ここで,``
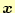 を直交化''という表記は,
を直交化''という表記は,
という操作を表す.(
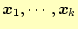 はすでに求められている固
有ベクトル)
はすでに求められている固
有ベクトル)
ホームページ: Yamamoto's laboratory
著者: 夏井拓也
natui takuya
平成17年12月22日
![]() の直交化は次の式で与えられる.
の直交化は次の式で与えられる.
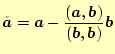
![]() だとする.
ここから,次に小さい固有値を求めようとする.この求めるべき固有ベクトルは,
だとする.
ここから,次に小さい固有値を求めようとする.この求めるべき固有ベクトルは,
![]() と直交していることが分かる.従って,これらの成分を抜き出しながら共役勾配
法で固有値を求めていけばよい.
と直交していることが分かる.従って,これらの成分を抜き出しながら共役勾配
法で固有値を求めていけばよい.